我校七年级数学兴趣小组成员们自主开展数学微项目研究.结合本阶段学内容特点,他们决定研究数的一些“神秘”性质.
| 探索数的神秘性质 | ||
| 素材 | 尼科马霍斯是古希腊数学家,他的著作《算术入门》中记载了各种数分门别类的整理成果,其中任何一个整数m的立方都可以写成m个连续奇数之和. | 举例论证: 13=1;23=3+5;33=7+9+11; 请你按规律写出: 43= 13+15+17+19 13+15+17+19 . |
| 规律总结 | 当m是奇数7时,则等号右边式子中的中间数(即第4个数)为 49 49 ; |
当m为偶数10时,则等号右边式子中的中间两个数(即第5和第6个数)为 99,101 99,101 . |
| 综合应用 | 利用上面结论计算:13+23+33+…+93+103+113. | |
| 拓展延伸 | 我们还发现以下规律:已知m≥2,n≥3,且m,n均为正整数,如果将mn进行如图所示的“分解”: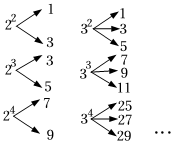 若mn(且m,n均为不大于7的正整数)的分解中有奇数31,则mn的值为 64或216 64或216 . |
|
【答案】13+15+17+19;49;99,101;64或216
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/7 9:0:8组卷:405引用:4难度:0.4
相似题
-
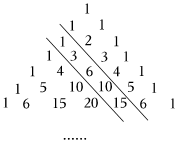 1.我国古代数学家杨辉发现了如图所示的三角形,后人称它为“杨辉三角”,它具有一定的规律性,从图中取一斜列数:1,3,6,10,15,我们把第一个数记为a1,第二个数记为a2,第三个数记为a3,…第n个数记为an,则an=.发布:2025/5/23 18:0:1组卷:121引用:3难度:0.7
1.我国古代数学家杨辉发现了如图所示的三角形,后人称它为“杨辉三角”,它具有一定的规律性,从图中取一斜列数:1,3,6,10,15,我们把第一个数记为a1,第二个数记为a2,第三个数记为a3,…第n个数记为an,则an=.发布:2025/5/23 18:0:1组卷:121引用:3难度:0.7 -
2.从1到2020连续自然数的平方和12+22+32+…+20202的个位数是( )
发布:2025/5/23 23:0:1组卷:190引用:2难度:0.5 -
3.观察以下等式:
第1个等式:,3+11=4+01
第2个等式:,5+12=5+12
第3个等式:,7+13=6+43
第4个等式:,9+14=7+94
…
按照以上规律,回答下列问题:
(1)写出第5个等式:;
(2)写出你猜想的第n个等式(用含n的式子表示),并证明.发布:2025/5/23 17:0:1组卷:36引用:1难度:0.7


