定义：有两个相邻的内角是直角，并且有两条邻边相等的四边形称为邻等四边形，相等两邻边的夹角称为邻等角．
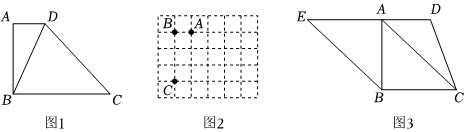
（1）如图1，在四边形ABCD中，AD∥BC，∠A=90°，对角线BD平分∠ADC．求证：四边形ABCD为邻等四边形．
（2）如图2，在6×5的方格纸中，A，B，C三点均在格点上，若四边形ABCD是邻等四边形，请画出所有符合条件的格点D．
（3）如图3，四边形ABCD是邻等四边形，∠DAB=∠ABC=90°，∠BCD为邻等角，连结AC，过B作BE∥AC交DA的延长线于点E．若AC=8，DE=10，求四边形EBCD的周长．
【考点】四边形综合题．
【答案】（1）证明过程见解答；
（2）图形见解答；
（3）38-6．
（2）图形见解答；
（3）38-6
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/6 8:0:9组卷：2744引用：7难度：0.1
相似题
-
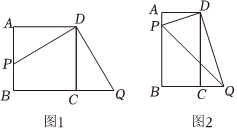1．（1）如图1，将直角三角板的直角顶点放在正方形ABCD上，使直角顶点与D重合，三角板的一边交AB于点P，另一边交BC的延长线于点Q．求证：DP=DQ；
（2）如图2，将（1）中“正方形ABCD”改成“矩形ABCD”，且DC=2DA，其他条件不变，试猜想DQ与DP的数量关系，并说明理由；
（3）在（2）的条件下，若PQ=10，DA=4，则AP的长度为 ．（直接写出答案）发布：2025/5/21 17:0:2组卷：60引用：2难度：0.5 -
2．【基础问题】
如图①，矩形ABCD中，点E为AB边上一点，连接DE，作EF⊥DE交BC于点F，且DE=FE，求证：△AED≌△BFE．
【拓展延伸】
（1）如图②，点E为平行四边形ABCD内部一点，EA=EB，DA⊥AE，作DF⊥BA交BA延长线于点F，若DA=2EA，AB=5，则平行四边形ABCD的面积为 ；
（2）如图③，在正方形ABCD中，AD=6，在CD边上取一点E，使EC=2DE，将△AED沿AE翻折到△AED′位置，作D′F⊥AB于点F，在D′F右侧作∠FGD'=90°，则△FGD'面积的最大值为 ．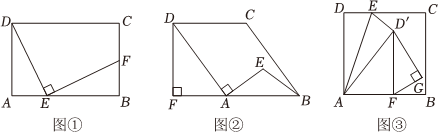
发布：2025/5/21 17:0:2组卷：160引用：1难度：0.3 -
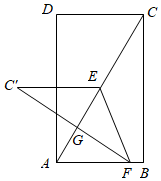3．如图，矩形ABCD中，AB=2，BC=4，连结对角线AC，E为AC的中点，F为AB边上的动点，连结EF，作点C关于EF的对称点C′，连结C′E，C′F，若△EFC′与△ACF的重叠部分（△EFG）面积等于△ACF的3，则BF=．14发布：2025/5/21 18:0:1组卷：1667引用：8难度：0.1
相关试卷
