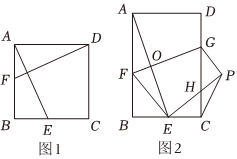
（1）如图1，在正方形ABCD中，点E、F分别在边BC和AB上，DF⊥AE于点O，求证：DF=AE．
（2）如图2，在矩形ABCD中，将矩形ABCD折叠，得到四边形FEPG，EP交CD于点H，点A落在BC边上的点E处，折痕交边AB于F，交边CD于G，连接AE交GF于点O，若
AD
AB
=
2
3
，且tan∠CGP=
3
4
，GF=2
10
，求AE与CP的长；

【答案】（1）证明见解析
（2）AE=3

，CP=

．

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/9/20 0:0:11组卷：11引用：1难度：0.7

相似题

1．某工厂要在一个正三角形ABC的钢板上切割一个四边形的材料DCEF来加工，若AB=2，DC=
2
3
，DC∥EF（如图），则四边形DCEF面积最大值为（　　）
A．
5
3
12
B．
4
3
9
C．
3
D．
5
2
发布：2024/9/26 2:0:2组卷：7引用：1难度：0.6
解析
2．若两个相似三角形的面积之比为2：3，则它们的对应边之比为（　　）
A．
2
3
B．
3
2
C．
6
3
D．
6
2
发布：2024/8/12 13:0:1组卷：4引用：1难度：0.9
解析
3．若两个相似三角形的周长之比为3：5，则这两个三角形的面积之比为（　　）
A．3：5 B．3：8 C．9：15 D．9：25
发布：2024/8/17 1:0:3组卷：7引用：1难度：0.9
解析

1．某工厂要在一个正三角形ABC的钢板上切割一个四边形的材料DCEF来加工，若AB=2，DC=23，DC∥EF（如图），则四边形DCEF面积最大值为（ ）