如图1，菱形ABCD中∠ABC=120°，动点E，F在边AD，AB上（不含端点），且存在实数λ使EF=λDB，沿EF将△AEF向上折起得到△PEF，使得平面PEF⊥平面BCDEF，如图2所示．
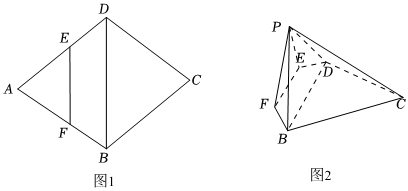
（1）若BF⊥PD，设三棱锥P-BCD和四棱锥P-BDEF的体积分别为V1，V2，求V1V2；
（2）当点E的位置变化时，平面EPF与平面BPF的夹角（锐角）的余弦值是否为定值，若是，求出该余弦值，若不是，说明理由；
EF
=
λ
DB
V
1
V
2
【考点】二面角的平面角及求法；棱柱、棱锥、棱台的体积．
【答案】（1）；
（2）是，．
9
5
（2）是，
5
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/20 6:0:3组卷：117引用：3难度：0.3
相似题
-
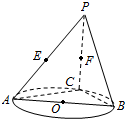1．如图，AB是圆O的直径，点C是圆O上异于A，B的点，直线PC⊥平面ABC，E，F分别是PA，PC的中点．
（Ⅰ）记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系，并加以证明；
（Ⅱ）设（Ⅰ）中的直线l与圆O的另一个交点为D，且点Q满足．记直线PQ与平面ABC所成的角为θ，异面直线PQ与EF所成的角为α，二面角E-l-C的大小为β．求证：sinθ=sinαsinβ．DQ=12CP发布：2025/1/20 8:0:1组卷：907引用：12难度：0.1 -
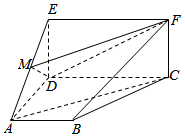2．如图，四边形ABCD为梯形，四边形CDEF为矩形，平面ABCD⊥平面CDEF，∠BAD=∠ADC=90°，AB=AD=DE=CD，M为AE的中点．12
（1）证明：AC∥平面MDF；
（2）求平面MDF与平面BCF的夹角的大小．发布：2025/1/2 8:0:1组卷：141引用：1难度：0.6 -
3．如图，AB是圆O的直径，PA垂直于圆所在的平面，C是圆周上的点．
（1）求证：平面PAC⊥平面PBC；
（2）若AB=2，AC=2，PA=2，求二面角C-PB-A的度数．2发布：2025/1/28 8:0:2组卷：33引用：1难度：0.5
