类比同类项的概念，我们规定：所含字母相同，并且相同字母的指数之差的绝对值都小于或等于1的项是“准同类项”．
例如：a3b4与2a4b3是“准同类项”．
（1）给出下列三个单项式：
①2a4b5，②3a2b5，③-4a4b4．
其中与a4b5是“准同类项”的是 ①③①③（填写序号）．
（2）已知A，B，C均为关于a,b的多项式，A=a4b5+3a3b4+（n-2）a2b3，B=2a2b3-3a2bn+a4b5，C=A-B．若C的任意两项都是“准同类项”，求n的值．
（3）已知D，E均为关于a,b的单项式，D=2a2bm，E=3anb4，其中m=|x-1|+|x-2|+k,n=k（|x-1|-|x-2|），x和k都是有理数，且k＞0．若D与E是“准同类项”，则x的最大值是 7272，最小值是 138138．
7
2
7
2
13
8
13
8
【答案】①③；；
7
2
13
8
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/26 18:0:2组卷：881引用：1难度：0.3
相似题
-
1．如果一个三位数m满足各个数位上的数字互不相同，且都不为零，那么称这个三位数为“互异数”．将“互异数”m的个位数字去掉，得到一个两位数m'，将其与m的个位数字的差记为F（m），将m的十位数字与个位数字的差记为G（m）．已知一个三位正整数m=20（5x+1）+2y（其中x、y都是整数，且1≤x≤9，1≤y≤9）是“互异数”，
为整数且能被13整除，则满足条件的“互异数”m的最大值 ．F（m）G（m）发布：2025/6/10 9:30:2组卷：301引用：4难度：0.7 -
2．计算：
（1）3（a2-ab）-5（ab+2a2-1）；
（2）3x2-[5x-（-3）+3x2]．12x发布：2025/6/10 15:30:2组卷：1383引用：2难度：0.6 -
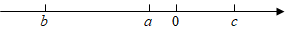3．实数a,b,c在数轴上的对应点如图所示，化简：．|a|+3（c-b）3-|a+b|+（a-c）2发布：2025/6/10 15:30:2组卷：139引用：6难度：0.7
