定义：在等腰三角形中，若有一条边是另一条边的2倍，则称这个三角形为倍腰三角形．
理解定义：若有一个倍腰三角形有一条边为2，求这个倍腰三角形的周长；
性质探究：判断下列关于倍腰三角形的说法是否正确，正确的打“√”；错误的打“×”；
（1）所有的倍腰三角形都是相似三角形√√
（2）若倍腰三角形的底角为α，则tanα=15√√
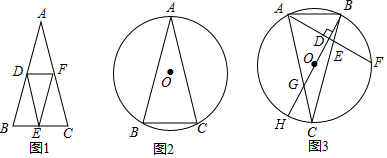
（3）如图1，依次连接倍腰三角形ABC各边的中点，则图1中共有4个倍腰三角形××
性质应用：如图2，倍腰三角形△ABC是⊙O的内接三角形，且AB=AC，若⊙O的半径为1，求倍腰三角形△ABC的面积；
拓展应用：如图3，⊙O是倍腰三角形△ABC的外接圆，直径BH⊥AF于点D，AF与BC相交于点E，AC与BH相交于点G，△ABE是倍腰三角形，其中AB=AE，BE=2．请直接写出CG的长．
15
【考点】圆的综合题．
【答案】√；√；×
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/18 5:0:8组卷：197引用：2难度：0.1
相似题
-
1．已知⊙O的直径AB=2，弦AC与弦BD交于点E，且OD⊥AC，垂足为点F．
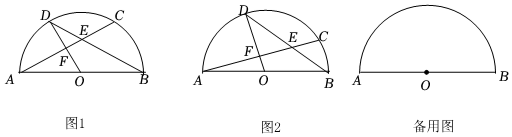
（1）如图1，若AC=BD，求线段DE的长．
（2）如图2，若DE：BE=3：2，求∠ABD的正切值．
（3）连结BC，CD，DA，若BC是⊙O的内接正n边形的一边，CD是⊙O的内接正2n边形的一边，求△ACD的面积．发布：2025/5/24 21:30:1组卷：239引用：1难度：0.3 -
2．在Rt△ABC中，∠C=90°．
（1）如图①，点O在斜边AB上，以点O为圆心，OB长为半径的圆交AB于点D，交BC于点E，与边AC相切于点F．求证：∠1=∠2；
（2）在图②中作⊙M，使它满足以下条件：
①圆心在边AB上；②经过点B；③与边AC相切．
（尺规作图，只保留作图痕迹，不要求写出作法）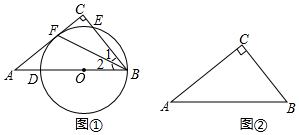
发布：2025/5/24 21:30:1组卷：833引用：9难度：0.3 -
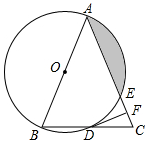3．如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC，垂足为点F．
（1）求证：直线DF是⊙O的切线；
（2）求证：BC2=4CF•AC；
（3）若⊙O的半径为4，∠CDF=15°，求阴影部分的面积．发布：2025/5/24 21:0:1组卷：2988引用：17难度：0.5
