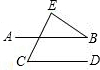
（1）模型：如图1，AD，BC交于O点．求证：∠D+∠C=∠A+∠B．
（2）模型应用：如图2，∠BAD和∠BCD的平分线交于点E．
①若∠D=20°，∠B=60°，则∠E的度数是 40°40°．
②直接写出∠E与∠D，∠B之间的数量关系是：∠E=12（∠B+∠D）∠E=12（∠B+∠D）．
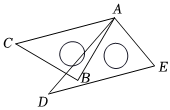
（3）类比应用：如图3，∠BAD的平分线AE与∠BCD的平分线CE交于点E．若∠D=m°，∠B=n°，（m＜n）．求∠E的度数．（用含有m,n的式子表示）
1
2
1
2
【答案】40°；∠E=（∠B+∠D）
1
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/26 6:0:3组卷：80引用：2难度：0.5
相似题
-
1．如图，已知AB∥CD，∠E=80°，∠B=30°，则∠C=．发布：2025/6/10 11:30:1组卷：132引用：10难度：0.9 -
2．如图，在△ABC中，AD⊥BC于D，AE平分∠BAC．
（1）若∠C=70°，∠B=30°，求∠DAE的度数；
（2）若∠C-∠B=20°，则∠DAE=；
（3）若∠C-∠B=α（∠C＞∠B），求∠DAE的度数（用含α的代数式表示）．发布：2025/6/10 7:30:1组卷：719引用：2难度：0.4 -
3．如图，∠ABC=∠ACB，AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF．以下结论：①AD∥BC；②∠ACB=2∠ADB；③∠ADC=90°-∠ABD；④∠BDC=∠BAC．其中正确的结论有（ ）发布：2025/6/10 9:0:1组卷：4058引用：25难度：0.7
