已知过抛物线C：y2=2px（p＞0）的焦点F，斜率为2的直线交抛物线于A（x1，y1），B（x2，y2）（x1＜x2）两点，且|AB|=6．
（1）求该抛物线C的方程；
（2）已知抛物线上一点M（t,4），过点M作抛物线的两条弦MD和ME，且MD⊥ME，判断直线DE是否过定点？并说明理由．
2
【考点】直线与抛物线的综合．
【答案】（1）y2=4x．
（2）直线DE过定点，证明如下：
由（1）可得点M（4，4），可得直线DE的斜率不为0，
设直线DE的方程为：x=my+t，
联立
，得y2-4my-4t=0，
则Δ=16m2+16t＞0①．
设D（x1，y1），E（x2，y2），则y1+y2=4m，y1y2=-4t．
∵MD•ME=（x1-4，y1-4）•（x2-4，y2-4）=x1x2-4（x1+x2）+16+y1y2-4（y1+y2）+16
=
==t2-16m2-12t+32-16m=0
即t2-12t+32=16m2+16m，得：（t-6）2=4（2m+1）2，
∴t-6=±2（2m+1），即t=4m+8或t=-4m+4，
代入①式检验均满足Δ＞0，
∴直线DE的方程为：x=my+4m+8=m（y+4）+8或x=m（y-4）+4．
∴直线过定点（8，-4）（定点（4，4）不满足题意，故舍去）．
（2）直线DE过定点，证明如下：
由（1）可得点M（4，4），可得直线DE的斜率不为0，
设直线DE的方程为：x=my+t，
联立
x = my + t |
y 2 = 4 x |
则Δ=16m2+16t＞0①．
设D（x1，y1），E（x2，y2），则y1+y2=4m，y1y2=-4t．
∵MD•ME=（x1-4，y1-4）•（x2-4，y2-4）=x1x2-4（x1+x2）+16+y1y2-4（y1+y2）+16
=
y
1
2
4
•
y
2
2
4
-
4
（
y
1
2
4
+
y
2
2
4
）
+
16
+
y
1
y
2
-
4
（
y
1
+
y
2
）
+
16
=
（
y
1
y
2
）
2
16
-
（
y
1
+
y
2
）
2
+
3
y
1
y
2
-
4
（
y
1
+
y
2
）
+
32
即t2-12t+32=16m2+16m，得：（t-6）2=4（2m+1）2，
∴t-6=±2（2m+1），即t=4m+8或t=-4m+4，
代入①式检验均满足Δ＞0，
∴直线DE的方程为：x=my+4m+8=m（y+4）+8或x=m（y-4）+4．
∴直线过定点（8，-4）（定点（4，4）不满足题意，故舍去）．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/13 8:0:9组卷：65引用：3难度：0.5
相似题
-
1．抛物线x2=4y的焦点为F，准线为l,A，B是抛物线上的两个动点，且满足AF⊥BF，P为线段AB的中点，设P在l上的射影为Q，则
的最大值是（ ）|PQ||AB|发布：2024/12/29 5:30:3组卷：455引用：7难度：0.5 -
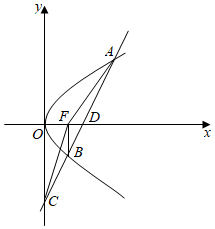2．如图，设抛物线y2=2px的焦点为F，过x轴上一定点D（2，0）作斜率为2的直线l与抛物线相交于A，B两点，与y轴交于点C，记△BCF的面积为S1，△ACF的面积为S2，若，则抛物线的标准方程为（ ）S1S2=14发布：2024/12/17 0:0:2组卷：163引用：6难度：0.6 -
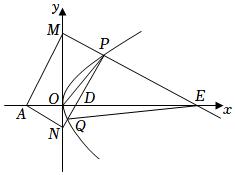3．如图，已知点P是抛物线C：y2=4x上位于第一象限的点，点A（-2，0），点M，N是y轴上的两个动点（点M位于x轴上方），满足PM⊥PN，AM⊥AN，线段PN分别交x轴正半轴、抛物线C于点D，Q，射线MP交x轴正半轴于点E．
（Ⅰ）若四边形ANPM为矩形，求点P的坐标；
（Ⅱ）记△DOP，△DEQ的面积分别为S1，S2，求S1•S2的最大值．发布：2024/12/29 1:0:8组卷：91引用：2难度：0.4
