阅读理解：
小明在做题时发现了一个规律：……
1
1
×
2
=
1
-
1
2
，

1
2
×
3
=
1
2
-
1
3
，

1
3
×
4
=
1
3
-
1
4
……
1
1
×
3
=
1
2
×
（
1
-
1
3
）
，

1
2
×
4
=
1
2
×
（
1
2
-
1
4
）
，

1
3
×
5
=
1
2
×
（
1
3
-
1
5
）
……
1
1
×
4
=
1
3
×
（
1
-
1
4
）
，

1
2
×
5
=
1
3
×
（
1
2
-
1
5
）
，

1
3
×
6
=
1
3
×
（
1
3
-
1
6
）
……
（1）猜测：
1
m
×
（
m
+
a
）
（a＞0）=
1
a
（
1
m
-
1
m
+
a
）
1
a
（
1
m
-
1
m
+
a
）
；
（2）请运用上面发现的规律计算下式的值．
①
1
1
×
2
+
1
2
×
3
+
1
3
×
4
+
...
+
1
9
×
10
；
②
1
1
×
3
+
1
3
×
5
+
1
5
×
7
+
...
+
1
19
×
21
；
③
1
1
×
5
+
1
5
×
9
+
1
9
×
13
+
...
+
1
2017
×
2021
．

【答案】

（

）

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/9/27 5:0:1组卷：88引用：1难度：0.5

相似题

1．阅读与应用计算：
1
1
×
2
+
1
2
×
3
+
1
3
×
4
+…+
1
9
×
10

解：因为：
1
1
×
2
=1-
1
2
，
1
2
×
3
=
1
2
-
1
3
，
1
3
×
4
=
1
3
-
1
4
，…
1
9
×
10
=
1
9
-
1
10

所以：
1
1
×
2
+
1
2
×
3
+
1
3
×
4
+…+
1
9
×
10
=（1-
1
2
）+（
1
2
-
1
3
）+（
1
3
-
1
4
）+…+（
1
9
-
1
10
）
=（1-
1
2
）+（
1
2
-
1
3
）+（
1
3
-
1
4
）+…+（
1
9
-
1
10
）=1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
+…
1
9
×
10
+
1
9
-
1
10

=1-
1
10
=
9
10

计算：①
1
1
×
2
+
1
2
×
3
+
1
3
×
4
+…+
1
2021
×
2022
；
②
1
1
×
3
+
1
3
×
5
+
1
5
×
7
+…+
1
49
×
51
．
发布：2025/6/14 3:30:2组卷：34引用：1难度：0.6
解析
2．下面是按一定规律得到的一列数．
第1个数：
1
2
-（1+
1
2
）=-1；第2个数：
1
3
-（1-
1
3
）=-
1
3
；
第3个数：
1
4
-（1+
1
4
）=-1；第4个数：
1
5
-（1-
1
5
）=
；
第5个数：
1
6
-（1+
1
6
）=-1；第6个数：
1
7
-（1-
1
7
）=
；…
（1）将上述内容进行填空；
（2）按照以上规律，用算式表示出第7，第8和第10个数；
（3）将（2）中的三个数用“＜”连接起来．
发布：2025/6/14 3:30:2组卷：33引用：2难度：0.5
解析
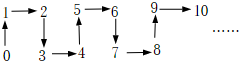3．探索规律：根据图中箭头指向的规律，从2031到2032再到2033，箭头的方向是（　　）
A． B． C． D．
发布：2025/6/14 3:30:2组卷：267引用：3难度：0.6
解析

3．探索规律：根据图中箭头指向的规律，从2031到2032再到2033，箭头的方向是（ ）