《几何原本》是古希腊数学家欧几里得创作的一部传世巨著，该书以基本定义、公设和公理作为推理的出发点，第一次实现了几何学的系绕化、条理化，成为用公理化方法建立数学演绎体系的最早典范．书中第Ⅰ卷第47号命题是著名的毕达哥拉斯（勾股定理），证明过程中以直角三角形ABC中的各边为边分别向外作了正方形（如图1）．某校数学兴趣小组对上述图形结构作拓广探究，提出了如下问题，请帮忙解答．
问题：如图2，已知△ABC满足AC=22，AB=2，设∠BAC=θ（0＜θ＜π），四边形ABGF、四边形ACED、四边形BCQP都是正方形．
（1）当θ=π2时，求EQ的长度；
（2）求AQ长度的最大值．
AC
=
2
2
θ
=
π
2
【考点】三角形中的几何计算．
【答案】（1）6；
（2）6．
（2）6．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/24 8:0:9组卷：144引用：8难度：0.5
相似题
-
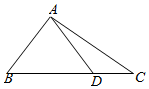1．如图，在△ABC中，已知B=45°，D是BC边上的一点，AD=4，AC=2，DC=2．7
（1）求cos∠ADC；
（2）求AB．发布：2024/12/29 12:0:2组卷：111引用：5难度：0.5 -
2．在△ABC中，角所对的边分别为a,b,c,给出下列四个命题中，其中正确的命题为（ ）
发布：2024/12/29 12:0:2组卷：188引用：14难度：0.6 -
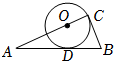3．如图，在Rt△ABC中，∠C=90°，O是边AC上一点，直线AB与圆O相切，切点为斜边的中点D，直线BC与圆O相切，若圆O的面积为π，则△ABC的面积为（ ）发布：2025/1/28 8:0:2组卷：41引用：1难度：0.7
