根据以下素材，探索完成任务．
| 如何设计实体店背景下的网上销售价格方案？ | ||
| 素材1 | 某公司在网上和实体店同时销售一种自主研发的小商品，成本价为40元/件． | |
| 素材2 | 据调查，该商品的网上销售价为60元/件时，平均每天销售量是200件，而销售价每降低x元（0x20），平均每天就可以多售出20x件． | |
| 素材3 | 该公司在实体店的销售价定为80元/件．据调查，该实体店的销售受网上影响，其销售量为（100-2x）件． | |
| 问题解决 | ||
| 任务1 | 确定函数模型 | ①求网上每天销售该商品的毛利润y（元）关于x的函数表达式． ②求该公司每天销售该商品的总毛利润W（元）关于x的函数表达式．（总毛利润=网上毛利润+实体店毛利润） |
| 任务2 | 探究函数最值 | 当该小商品的网上销售价是每件多少元时，该公司每天销售这种小商品的总毛利润最大？最大总毛利润是多少？ |
| 任务3 | 拟定价格方案 | 经综合分析，该公司认为总毛利润在 814 0 + 10 - 10 |
【考点】二次函数的应用．
【答案】任务1：①y=-20x2+200x+4000；
②W=-20x2+120x+8000；
任务2：当网上销售价是每件57元时，该公司每天销售这种小商品的总毛利润最大，最大总毛利润是8180元；
任务3：答案不唯一：当x符合1.5≤（x-3）2≤2.5均可．如网上销售价格为58.5元（或55.5元），总毛利润为8135元等．
②W=-20x2+120x+8000；
任务2：当网上销售价是每件57元时，该公司每天销售这种小商品的总毛利润最大，最大总毛利润是8180元；
任务3：答案不唯一：当x符合1.5≤（x-3）2≤2.5均可．如网上销售价格为58.5元（或55.5元），总毛利润为8135元等．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/24 15:0:10组卷：150引用：2难度：0.5
相似题
-
1．“贵妃芒”芒果品种是广受各地消费者青睐的优质新品种，在我国海南省广泛种植，某水果商以每斤15元的价格从该省批发“贵妃芒”，再按每斤25元价格到市区销售，平均每天可售出60斤，经过调查发现，如果每斤“贵妃芒”的售价每降低1元，那么平均每天的销售量会增加10斤，为了尽快减少库存，该水果商决定降价销售．设“贵妃芒”每斤的价格降低x元．
（1）则每天的销售量是 斤（用含x的代数式表示）；
（2）水果商销售“贵妃芒”每天盈利630元，每斤“贵妃芒”的售价应降至每斤多少元？（其他成本忽略不计）
（3）若x的范围为1≤x≤9的正整数，请直接写出水果商的最高利润与最低利润的差为 元．发布：2025/6/8 2:30:2组卷：430引用：2难度：0.5 -
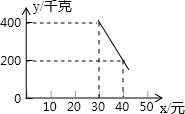2．某超市以20元/千克的进货价购进了一批绿色食品，如果以30元/千克销售这些绿色食品，那么每天可售出400千克．由销售经验可知，每天的销售量y（千克）与销售单价x（元）（x≥30）存在如图所示的一次函数关系．
（1）试求出y与x的函数关系式；
（2）设该超市销售该绿色食品每天获得利润w元，当销售单价为何值时，每天可获得最大利润？最大利润是多少？发布：2025/6/7 21:0:1组卷：626引用：5难度：0.6 -
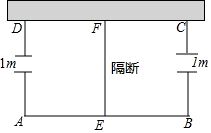3．如图所示，利用一面墙（墙的长度足够），用篱笆围成一个形如矩形ABCD的场地，在AD，BC边上各有一个宽为1m的缺口，在场地中有用篱笆做的隔断EF，且EF⊥AB，AB＞EF，已知所用篱笆总长度为38m.
（1）设隔断EF的长为x（m），请用含x的代数式表示AB的长．
（2）所围成形如矩形ABCD的场地的面积为100m2时，求AB的长．
（3）所围成矩形ABCD场地的面积能否为140m2？若能，求AB的长；若不能，说明理由．并写出所围成的矩形ABCD场地面积的最大值．发布：2025/6/8 2:0:5组卷：885引用：7难度：0.3
