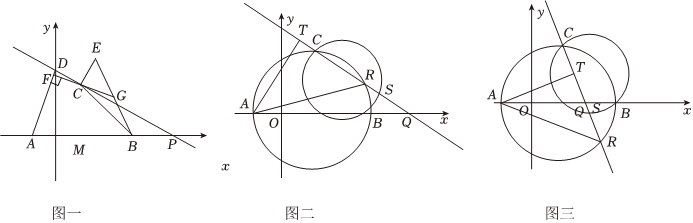
如图，平面直角坐标系中，以M（2，0）为圆心的⊙M交x轴于A、B两点，点A在点B左侧，且过C（2，4）．（1）求⊙M的半径及点A、B的坐标；
（2）如图一，点P（10，0），连接PC并延长，交y轴于点D，线段CD绕点C顺时针旋转90°得CE，连接EB、AD，过点C作AD的垂线交AD于点F，反向延长CF交BE于点G，求△ECG的面积；
（3）以BC为直径画圆，记为⊙N，x轴正半轴一动点Q坐标记为（m,0）．
①如图二，m＞6时，连接CQ交⊙M于点R，交⊙N于点S，作AT⊥CQ于T，求证：TC=RS；
②如图三，-2＜m＜6时，①中的结论还成立吗？若成立，请证明；若不成立，请说明理由．
【考点】圆的综合题．
【答案】（1）⊙M的半径为4，A（-2，0），B（6，0）；
（2）S△ECG=3；
（3）①证明见解答；
②TC=RS仍然成立．证明见解答．
（2）S△ECG=3；
（3）①证明见解答；
②TC=RS仍然成立．证明见解答．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/13 11:0:2组卷：112引用：1难度：0.2
相似题
-
1．【问题探究】
（1）如图1，在△ABC中，过点A作AD⊥BC于点D，AB=CD=5，BD=3，则S△ABC=；
（2）如图2，四边形ABDC是⊙O的内接四边形，BC是直径，AC=2，BC=4，=ˆBD，求四边形ABDC的面积；ˆDC
【问题解决】
（3）如图3，某广场有一个圆形草坪⊙O，为迎接全运会的到来，管理部门欲在⊙O中规划出一个四边形ABCD区域，用来种植景观桃树与月季，其中点A、B、C、D均在⊙O上，AB=120m,AD=20m,∠ADC=120°，∠BAD=90°．根据设计要求，需在BC上找一点Q，在AB上找一点P，满足PB=QC，沿PQ铺一条水管用于灌溉，且在△PBQ区域种植月季，在五边形APQCD区域种植景观桃树，设BP的长为x（m），△PBQ的面积为y（m2）．3
①求y与x之间的函数关系式；
②已知每平方米种植景观桃树的费用比每平方米种植月季的费用要贵，为节省成本，要求种植景观桃树区域的面积尽可能小，问种植景观桃树区域的面积是否存在最小值，若存在，请求出种植景观桃树区域面积的最小值，若不存在，请说明理由．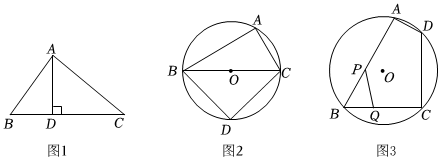
发布：2025/5/23 1:0:1组卷：144引用：1难度：0.3 -
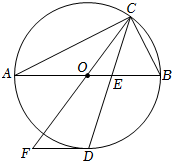2．如图，点C在以AB为直径的⊙O上，CD平分∠ACB交⊙O于点D，交AB于点E，过点D作⊙O的切线交CO的延长线于点F．
（1）求证：FD∥AB；
（2）若AC=2，BC=5，求FD的长．5发布：2025/5/23 0:30:1组卷：2147引用：13难度：0.2 -
3．在平面直角坐标系xOy中，已知点M（a,b），N．
对于点P给出如下定义：将点P向右（a≥0）或向左（a＜0）平移|a|个单位长度，再向上（b≥0）或向下（b＜0）平移|b|个单位长度，得到点P'，点P'关于点N的对称点为P″，NP″中点记为Q，称点Q为点P的“对应点”．
（1）如图，点M（1，1），点N在线段OM的延长线上，若点P（-3，0），点Q为点P的“对应点”．
①在图1中画出点Q；
②连接PQ，交线段ON于点T．求证：；NT=13OM
（2）⊙O的半径为2，M是⊙O上一点，点N在线段OM上，且ON=t（1＜t＜2），若P为⊙O外一点，点Q为点P的“对应点”，连接PQ．当点M在⊙O上运动时，直接写出PQ长的最大值与最小值的差（用含t的式子表示）．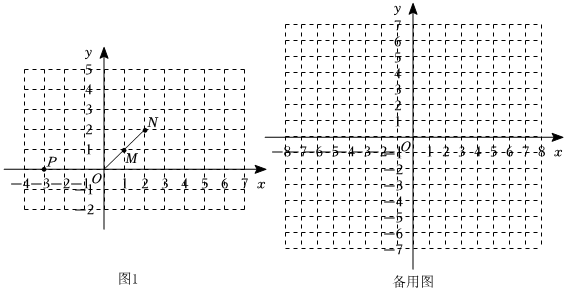
发布：2025/5/23 0:0:1组卷：176引用：1难度：0.3
