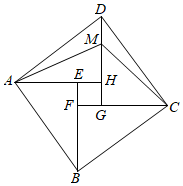
本期，我们学习了用赵爽弦图证明勾股定理．在如图所示的赵爽弦图中，在DH上取点M使得DM=GH，连接AM、CM．若正方形EFGH的面积为6，则△ADM与△CDM的面积之差为（　　）

A．3

B．2

C．

D．不确定

【答案】A

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/8/29 15:0:9组卷：993引用：6难度：0.5

相似题

1．如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形．如果AB=10，EF=2，那么AH等于
．
发布：2025/6/23 0:0:1组卷：9105引用：71难度：0.7
解析
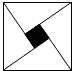2．如图，是由四个直角边分别为3和4全等的直角三角形拼成的“赵爽弦图”，那么阴影部分面积为

．
发布：2025/6/24 12:30:2组卷：896引用：13难度：0.9
解析
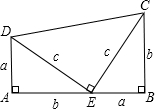3．历史上对勾股定理的一种证法采用了下列图形：其中两个全等的直角三角形边AE、EB在一条直线上．证明中用到的面积相等关系是（　　）
A．S_△EDA=S_△CEB
B．S_△EDA+S_△CEB=S_△CDE
C．S_{四边形CDAE}=S_{四边形CDEB}
D．S_△EDA+S_△CDE+S_△CEB=S_{四边形ABCD}
发布：2025/6/21 17:0:2组卷：1052引用：15难度：0.7
解析

1．如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形．如果AB=10，EF=2，那么AH等于．