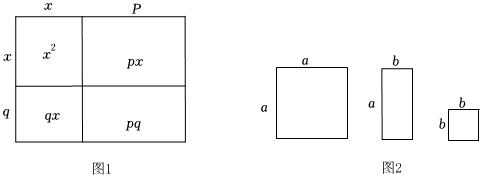
将几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,例如,由图1可得等式:x2+(p+q)x+pq=(x+p)(x+q).将图2所示的卡片若干张进行拼图,可以将二次三项式a2+3ab+2b2分解因式为( )
【答案】C
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/5/27 14:0:0组卷:879引用:10难度:0.7
相似题
-
1.阅读下列解答过程,并仿照解决问题:
已知x2-2x-3=0,求x3+x2-9x-8的值.
解:∵x2-2x-3=0,
∴x2=2x+3,
∴x3+x2-9x-8=x•x2+x2-9x-8=x•(2x+3)+(2x+3)-9x-8=2x2+3x+2x+3-9x-8=2(2x+3)-4x-5=1.
请你仿照上题的解法完成下题:x2-5x+1=0,求x3-4x2-4x-1的值.发布:2025/6/13 5:30:2组卷:262引用:3难度:0.9 -
2.我们经常利用完全平方公式以及变形公式进行代数式变形.已知关于a的代数式A=a2+a,请结合你所学知识,判断下列说法:①当a=-2时,A=2;②无论a取任何实数,不等式
恒成立;③若A-1=0,则A+14≥0;④已知代数式A、B、C满足a2+1a2=3,则A2+B2+C2-AB-AC-BC=15.正确的有( )A-B=2+3,B-C=2-3发布:2025/6/13 3:30:1组卷:204引用:1难度:0.6 -
3.若a+b=3,ab=-1,则代数式a3b+2a2b2+ab3的值为 .
发布:2025/6/13 0:0:2组卷:1267引用:6难度:0.5


