问题背景：
在△ABC中，AB、BC、AC三边的长分别为5、10、13，求这个三角形的面积．
小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），然后在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处，AB=22+12=5，BC=10，AC=13），如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种求△ABC面积的方法叫做构图法．
（1）请你将△ABC的面积直接填写在横线上：3.53.5．
思维拓展：
（2）若△ABC三边的长分别为5a、22a、17a（a＞0），请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
探索创新：
（3）若△ABC三边的长分别为m2+16n2、9m2+4n2、2m2+n2（m＞0，n＞0，且m≠n），求这个三角形的面积．
（4）直接写出当x为何值时，函数y=x2+9+（12-x）2+4有最小值，最小值是多少？
5
10
13
2
2
+
1
2
5
10
13
5
2
17
m
2
+
16
n
2
9
m
2
+
4
n
2
m
2
+
n
2
x
2
+
9
（
12
-
x
）
2
+
4
【答案】3.5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/16 12:0:1组卷：282引用：2难度：0.3
相似题
-
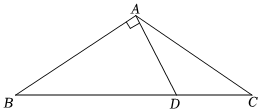1．如图在△ABC中，∠B=30°，AD=CD，AD⊥AB，垂足为A，AD=1cm,求AB长及△ABC的面积．发布：2025/6/9 5:0:1组卷：9引用：2难度：0.6 -
2．已知△ABC的面积为S，根据下列条件完成填空．
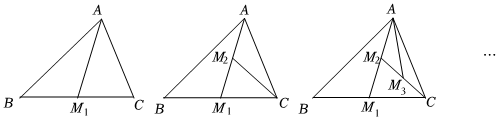
图1图2图3
（1）AM1是△ABC的边BC上的中线，如图1，则△ACM1的面积为 （用含S的式子表示，下同）；CM2是△ACM1的边AM1上的中线，如图2，则△ACM2的面积为 ；AM3是△ACM2的边CM2上的中线，如图3，则△ACM3的面积为 ；……
（2）在图2022中，CM2022是△ACM2021的边AM2021上的中线，则△ACM2022的面积为 ．发布：2025/6/9 5:0:1组卷：226引用：3难度：0.5 -
3．能将三角形面积平分的是三角形的（ ）
发布：2025/6/9 6:30:1组卷：804引用：64难度：0.9
