【教材呈现】
已知a+b=5，ab=3，求（a-b）2的值．
【例题讲解】
同学们探究出解这道题的两种方法：
| 方法一 | 方法二 |
| ∵（a+b）2=a2+2ab+b2 ∴a2+b2=（a+b）2-2ab ∵a+b=5，ab=3， ∴a2+b2=25-6=19 ∵（a-b）2=a2-2ab+b2 ∴（a-b）2=19-6=13 |
∵（a+b）2=a2+2ab+b2， ∵（a-b）2=a2-2ab+b2， ∴（a-b）2=（a+b）2- 4ab 4ab ∵a+b=5，ab=3， ∴（a-b）2=13． |
【方法运用】
（2）解答以下问题：
已知
a
+
1
a
=
4
（
a
-
1
a
）
2
【拓展提升】
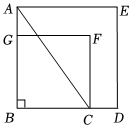
（3）如图，以Rt△ABC的直角边AB，BC为边作正方形ABDE和正方形BCFG．若△ABC的面积为5，正方形ABDE和正方形BCFG面积和为36，求AG的长度．
【考点】完全平方公式的几何背景．
【答案】4ab
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：639引用：4难度：0.7
相似题
-
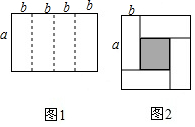1．如图1是一个宽为a、长为4b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图2）．
（1）观察图2，请你用等式表示（a+b）2，（a-b）2，ab之间的数量关系：；
（2）根据（1）中的结论．如果x+y=5，xy=，求代数式（x-y）2的值；94
（3）如果（2019-m）2+（m-2020）2=7，求（2019-m）（m-2020）的值．发布：2025/6/7 23:0:2组卷：1097引用：5难度：0.6 -
2．如图，将一张长方形纸板按图中虚线剪成九块，其中有两块是边长为m的大正方形，两块是边长都为n的小正方形，五块是长为m,宽为n的小长方形，且m＞n（以上长度单位：cm）
（1）观察图形，请根据大长方形的面积，写出一个正确的等式 ；
（2）若每块小长方形的面积为10cm2，四个正方形的面积和为58cm2，试求图中所有裁剪线（虚线部分）长之和．发布：2025/6/8 1:30:1组卷：60引用：1难度：0.5 -
3．正方形的边长增加了2cm,面积相应增加了24cm2，则这个正方形原来的面积是（ ）
发布：2025/6/8 6:0:2组卷：1745引用：11难度：0.8
