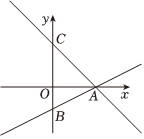
如图，直线y=12x-2分别交x轴，y轴于点A，点B，点C在y轴正半轴上，且OC=OA，点D（-2，m）在直线AC上，点P是x轴上的一个动点，设点P横坐标为t.
（1）求直线AC的函数解析式；
（2）连接PC，PD，若△CDP面积等于△ABC面积的12，求t的值；
（3）求22AP+BP的最小值．
1
2
1
2
2
2
【考点】一次函数综合题．
【答案】（1）直线AB的解析式为y=-x+4；
（2）10或-2；
（3）3．
（2）10或-2；
（3）3
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/29 8:0:9组卷：189引用：2难度：0.3
相似题
-
1．如图1，在平面直角坐标系中，直线
分别与x轴、y轴交于点A点和B点，过O点作OD⊥AB于D点，以OD为边构造等边△EDF（F点在x轴的正半轴上）．l：y=-33x+43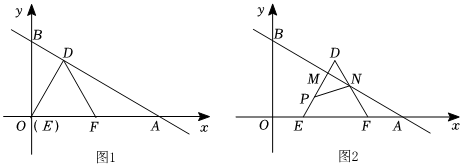
（1）求A、B点的坐标，以及OD的长；
（2）将等边△EDF，从图1的位置沿x轴的正方向以每秒1个单位的长度平移，移动的时间为t（s），同时点P从E出发，以每秒2个单位的速度沿着折线ED-DF运动（如图2所示），当P点到F点停止，△DEF也随之停止．
①t=（s）时，直线l恰好经过等边△EDF其中一条边的中点；
②当点P在线段DE上运动，若DM=2PM，求t的值；
③当点P在线段DF上运动时，若△PMN的面积为，求出t的值．3发布：2025/5/24 3:30:1组卷：471引用：2难度：0.2 -
2．将一个直角三角形纸片ABO，放置在平面直角坐标系中，点A（，0），点B（0，3），点O（0，0）3
（1）过边OB上的动点D（点D不与点B，O重合）作DE丄OB交AB于点E，沿着DE折叠该纸片，点B落在射线BO上的点F处．
①如图，当D为OB中点时，求E点的坐标；
②连接AF，当△AEF为直角三角形时，求E点坐标；
（2）P是AB边上的动点（点P不与点B重合），将△AOP沿OP所在的直线折叠，得到△A′OP，连接BA′，当BA′取得最小值时，求P点坐标（直接写出结果即可）．发布：2025/5/24 8:0:1组卷：843引用：2难度：0.3 -
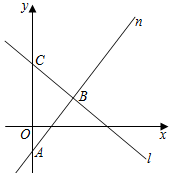3．在如图的平面直角坐标系中，直线n过点A（0，-2），且与直线l交于点B（3，2），直线l与y轴交于点C．
（1）求直线n的函数表达式；
（2）若△ABC的面积为9，求点C的坐标；
（3）若△ABC是等腰三角形，求直线l的函数表达式．发布：2025/5/24 9:0:1组卷：6355引用：10难度：0.1
