如图1，在△ABC中，BA=BC，D、E是AC边上的两点，且满足∠DBE=12∠ABC．以点B为旋转中心，将△CBE按逆时针方向旋转得到△ABF，连接DF．
（1）求证：DF=DE；
（2）如图2，若AB⊥BC，其他条件不变，探究AD，DE，EC之间的关系，并证明．
1
2
【考点】旋转的性质；全等三角形的判定与性质．
【答案】（1）证明过程见解答；
（2）AD2+CE2=DE2，证明过程见解答．
（2）AD2+CE2=DE2，证明过程见解答．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/30 8:0:9组卷：742引用：3难度：0.4
相似题
-
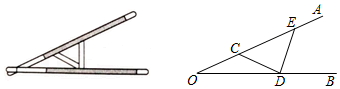
1．“三等分角”大约是在公元前五世纪由古希腊人提出来的．借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D，E可在槽中滑动，若∠O=25°，则∠BDE的度数是 ．
发布：2025/6/15 16:30:1组卷：118引用：1难度：0.5 -
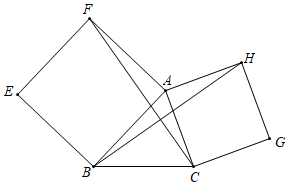2．1．如图所示，在△ABC中，以AB，AC为边分别作正方形AFEB和正方形ACGH，连接FC，BH．
（1）利用旋转的观点，在此题中△AFC绕着点 旋转 度可得到△．
（2）CF与BH相等吗？请说明理由．
（3）CF 与BH垂直吗？请说明理由．发布：2025/6/15 20:30:5组卷：129引用：2难度：0.5 -
3．如图，桌面上的木条b、c固定，木条a在桌面上绕点O旋转n°（0＜n＜90）后与b垂直，则n=（ ）发布：2025/6/15 15:0:1组卷：174引用：2难度：0.7
