在△ABC中，∠BAC=90°，AB=AC，直线l经过点A，过点B、C分别作l的垂线，垂足分别为点D、E．
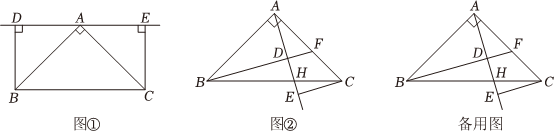
（1）特例体验：
如图①，若直线l∥BC，AB=AC=2，分别求出线段BD、CE和DE的长；
（2）规律探究：
如图②，若直线l从图①状态开始绕点A顺时针旋转a（45°＜α＜90°），与线段BC相交于点H，请再探线段BD、CE和DE的数量关系并说明理由；
（3）尝试应用：
在图②中，延长线段BD交线段AC于点F，若CE=3，DE=1，求S△BFC．
AB
=
AC
=
2
【考点】几何变换综合题．
【答案】（1）BD=CE=1，DE=2；
（2）DE=BD-CE，理由见解答．
（3）．
（2）DE=BD-CE，理由见解答．
（3）
25
8
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/19 8:0:9组卷：95引用：1难度：0.3
相似题
-
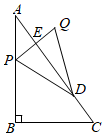1．如图，在△ABC中，∠ABC=90°，AB=4，BC=3．点P从点A出发，沿折线AB-BC以每秒5个单位长度的速度向点C运动，同时点D从点C出发，沿CA以每秒2个单位长度的速度向点A运动，点P到达点C时，点P、D同时停止运动．当点P不与点A，C重合时，作点P关于直线AC的对称点Q，连接PQ交AC于点E，连接DP、DQ．设点P的运动时间为t秒．
（1）当点P与点B重合时，求t的值；
（2）用含t的代数式表示线段CE的长；
（3）当△PDQ为等腰直角三角形时，求t的值．发布：2025/5/25 12:30:1组卷：196引用：4难度：0.3 -
2．【问题提出】
（1）如图①，在矩形ABCD中，点P、Q分别在线段AD、BC上，点B与点E关于PQ对称，点E在线段AD，连接BP、EQ、PQ交BE于点O，则四边形PBQE的形状是 ；
【问题探究】
（2）如图②，在矩形ABCD中，AB=3，点P、Q分别在线段AB、BC上，点B与点E关于PQ对称，点E在线段AD上，，求PQ的长；AE=5
【问题解决】
（3）如图③，有一块矩形空地ABCD，AB=60m,BC=80m,点P是一个休息站且在线段AB上，AP=40m,点Q在线段BC上，现要在点B关于PQ对称的点E处修建口水井，并且修建水渠AE和CE，以便于在四边形空地AECD上种植花草，余下部分贴上地砖．种植花草的四边形空地AECD的面积是否存在最小值，若存在，请求出最小值，若不存在，请说明理由．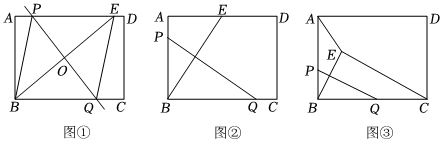
发布：2025/5/25 13:0:1组卷：154引用：1难度：0.2 -
3．如图，在正方形纸片ABCD中，点E为正方形CD边上的一点（不与点C，点D重合），将正方形纸片折叠，使点A落在点E处，点B落在点F处，EF交BC于点H，折痕为GM，连接AE、AH，AH交GM于点K．下列结论：①△AME是等腰三角形；②AE=MG；③AE平分∠DEF；④AE=AH；⑤∠EAH=45°，其中正确结论的个数是（ ）发布：2025/5/25 13:30:1组卷：470引用：4难度：0.1
