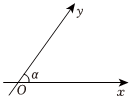
如图，当∠xOy=α[α∈（0，π2）∪（π2，π）]时，定义平面坐标系xOy为α-仿射坐标系，在α-仿射坐标系中，任意一点M的斜坐标这样定义：若OM=xe1+ye2，其中e1，e2分别为与x轴、y轴正方向相同的单位向量，则M的斜坐标为（x,y）．在α-仿射坐标系中，若α=π3，M的斜坐标为（2，-1），则O到M的距离为（ ）
∠
x
O
y
=
α
[
α
∈
（
0
，
π
2
）
∪
（
π
2
，
π
）
]
OM
=
x
e
1
+
y
e
2
e
1
e
2
π
3
【考点】平面向量的基本定理．
【答案】B
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：49引用：1难度：0.7
