如图1，已知线段AB、CD相交于点O，连接AC、BD，则我们把形如这样的图形称为“8字型”．
（1）求证：∠A+∠C=∠B+∠D；
（2）如图2，若∠CAB和∠BDC的平分线AP和DP相交于点P，与CD、AB分别相交于点M、N．
①以线段AC为边的“8字型”有 33个，以点O为交点的“8字型”有 44个；
②若∠B=100°，∠C=120°，求∠P的度数；
③根据②的结果直接写出∠B、∠C、∠P之间的关系（不需要证明）．
【考点】三角形内角和定理．
【答案】3；4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/28 15:0:8组卷：208引用：1难度：0.6
相似题
-
1．我们将内角互为对顶角的两个三角形称为“对顶三角形”．例如，在图1中，△AOB的内角∠AOB与△COD的内角∠COD互为对顶角，则△AOB与△COD为“对顶三角形”，根据三角形内角和定理知“对顶三角形”有如下性质：∠A+∠B=∠C+∠D．
（1）如图1，在“对顶三角形”△AOB与△OOD中，∠AOB=70°，则∠C+∠D=°．
（2）如图2，在△ABC中，AD、BE分别平分∠BAC和∠ABC，若∠C=60°，∠ADE比∠BED大6°，求∠BED的度数．
发布：2025/5/24 11:0:1组卷：826引用：3难度：0.5 -
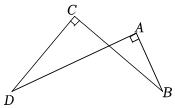2．如图，∠C=∠A=90°，∠B=25°，则∠D的度数是（ ）发布：2025/5/24 13:30:2组卷：831引用：5难度：0.6 -
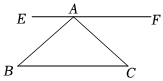3．如图所示，能利用图中作法：过点A作BC的平行线，证明三角形内角和是180°的原理是（ ）发布：2025/5/24 10:0:2组卷：112引用：3难度：0.7
