下列结论中，矩形具有而平行四边形不一定具有的性质是（ ）
【答案】D
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/13 8:0:8组卷：449引用：6难度：0.8
相似题
-
1．已知四边形ABCD为矩形，对角线AC，BD交于点O，点E在∠BDC的平分线上，连接EC．若2∠DCE+∠OAD=90°，则点E一定也在（ ）
发布：2025/5/26 2:0:6组卷：185引用：2难度：0.6 -
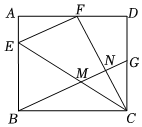2．如图，在矩形ABCD中，点E在边AB上，△BEC与△FEC关于直线EC对称，点B的对称点F在边AD上，G为CD中点，连结BG分别与CE，CF交于M，N两点．若BM=BE，MG=1，则CG的长为 ，NG的值为 ．发布：2025/5/26 0:0:1组卷：106引用：2难度：0.5 -
3．感知：如图①，▱ABCD的对角线AC，BD相交于点O，DE∥AC，CE∥BD，则四边形OCED是平行四边形（不需要证明）．
拓展：如图②，矩形ABCD的对角线AC，BD相交于点O，DE∥AC，CE∥BD，则四边形OCED是什么样的特殊四边形，请说明理由．
应用：如图③，菱形ABCD的对角线AC，BD相交于点O，∠ABC=60°，BC=4，DE∥AC交BC的延长线于点F，CE∥BD．求四边形ABFD的周长．
发布：2025/5/26 1:0:1组卷：519引用：7难度：0.3
