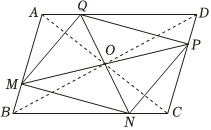
如图，▱ABCD的对角线交于点O，M，N，P，Q分别是▱ABCD四条边上不重合的点．现有甲、乙、丙三种方案，则能判定四边形MNPQ是平行四边形的是（ ）
甲：使AQ=CN，AM=CP；
乙：使MP，NQ均经过点O；
丙：使NQ经过点O，且AM=DP
【考点】平行四边形的判定与性质；全等三角形的判定与性质．
【答案】A
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/29 8:0:10组卷：256引用：1难度：0.5
相似题
-
1．在△ABC中，∠C=90°，D是AC的中点，E是AB的中点，作EF⊥BC于F，延长BC至G，使CG=BF，连接CE、DE、DG．
（1）如图1，求证：四边形CEDG是平行四边形；
（2）如图2，连接EG交AC于点H，若EG⊥AB，请直接写出图2中所有长度等于GH的线段．2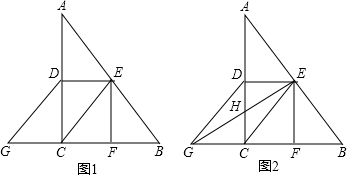
发布：2025/5/23 16:0:1组卷：852引用：6难度：0.3 -
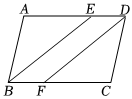2．如图，四边形ABCD是平行四边形，E、F分别是边AD、BC上的点，且AE=CF．
求证：四边形BEDF是平行四边形．
证明：
∵四边形ABCD是平行四边形，
∴……
∵AE=CF
∴DE=BF
∵DE∥BF
∴四边形BEDF是平行四边形
省略号表示的是（ ）发布：2025/5/23 22:0:2组卷：262引用：5难度：0.7 -
3．如图，已知▱ABCD，点E，F在对角线AC上，且AE=CF，连接DE，DF，BE，BF．求证：四边形DEBF为平行四边形．以下是排乱的证明过程：
①∴四边形DEBF为平行四边形；
②∵四边形ABCD为平行四边形，∴OD=OB，OA=OC；
③连接BD，交AC于点O；
④∵AE=CF，∴OA-AE=OC-CF，即OE=OF，证明步骤正确的顺序是（ ）发布：2025/5/23 17:0:1组卷：234引用：2难度：0.5
