勾股定理是几何学中的明珠，充满着魅力．千百年来，人们对它的证明趋之若鹜，其中有著名的数学家，也有业余数学爱好者．向常春在1994年构造发现了一个新的证法．证法如下：
把两个全等的直角三角形（Rt△ACB≌Rt△DAE）如图1放置，∠DAB=∠B=90°，AC⊥DE点E在边AC上，现设Rt△ACB两直角边长分别为CB=b、AB=a,斜边长为AC=c,请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积，再探究这三个图形面积之间的关系，可得到勾股定理．
（1）请根据上述图形的面积关系证明勾股定理；
（2）如图2，铁路上A、B两点（看作直线上的两点）相距40千米，CD为两个村庄（看作直线上的两点），AD⊥AB，BC⊥AB，垂足分别为A、B，AD=25千米，BC=16千米，则两个村庄的距离为 4141千米；
（3）在（2）的背景下，若AB=40千米，AD=25千米，BC=16千米，要在AB上建造一个供应站P，使得PC=PD，请用尺规作图在图2中作出P点的位置并求出AP的距离；
（4）借助上面的思考过程，当1＜x＜11时，求代数式x2-2x+5+x2-22x+130的最小值．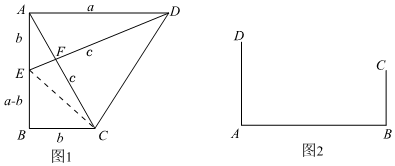
x
2
-
2
x
+
5
+
x
2
-
22
x
+
130
【考点】三角形综合题．
【答案】41
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/4 11:0:13组卷：266引用：3难度：0.3
相似题
-
1．某兴趣小组探索等腰三角形中线段比值问题，部分探索活动如下：
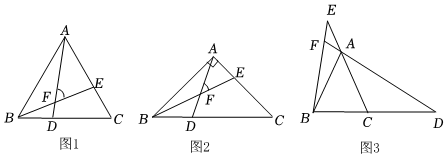
（1）如图1，在△ABC中，AB=AC，∠ABC=60°，D，E分别是BC，AC边上的点，∠AFE=∠ABC，则的值为 ．BEAD
（2）如图2，在△ABC中，AB=AC，∠ABC=45°，D，E分别是BC，AC边上的点，∠AFE=∠ABC，请你猜想的值，并给出证明；BEAD
（3）如图3，在△ABC中，AB=AC，，D，E分别是BC，CA边延长线上的点，∠DFB=∠ABC，请直接写出cos∠ABC=512的值．BEAD发布：2025/5/26 0:0:1组卷：153引用：1难度：0.4 -
2．在△ABC中，AB=AC，BC=12，E为边AC的中点，
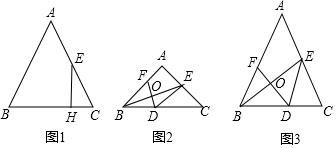
（1）如图1，过点E作EH⊥BC，垂足为点H，求线段CH的长；
（2）作线段BE的垂直平分线分别交边BC、BE、AB于点D、O、F．
①如图2，当∠BAC=90°时，求BD的长；
②如图3，设tan∠ACB=x,BD=y,求y与x之间的函数表达式和tan∠ACB的最大值．发布：2025/5/26 1:0:1组卷：278引用：2难度：0.1 -
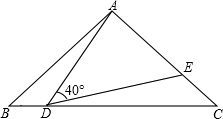3．如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E．
（1）当∠BDA=115°时，∠BAD=°，∠DEC=°；
（2）当DC等于多少时，△ABD与△DCE全等？请说明理由；
（3）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数．若不可以，请说明理由．发布：2025/5/26 2:30:2组卷：976引用：8难度：0.3
