设{a，b，c}为空间一组基底，若向量p=xa+yb+zc，则向量p在基底{a，b，c}下的坐标为（x,y,z）．若q在基底{a，b，c}下的坐标为（2，3，4），则向量q在基底{a-b，b-c，c+a}下的坐标为（ ）
{
a
，
b
，
c
}
p
=
x
a
+
y
b
+
z
c
p
{
a
，
b
，
c
}
q
{
a
，
b
，
c
}
q
{
a
-
b
，
b
-
c
，
c
+
a
}
【考点】空间向量基底表示空间向量．
【答案】C
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：129引用：2难度：0.6
相似题
-
1．17世纪，笛卡尔在《几何学》中，通过建立坐标系，引入点的坐标的概念，将代数对象与几何对象建立关系，从而实现了代数问题与几何问题的转化，打开了数学发展的新局面，创立了新分支——解析几何．我们知道，方程x=1在一维空间中表示一个点；在二维空间中，它表示一条直线；在三维空间中，它表示一个平面．那么，过点P0（1，2，1）且以
=（-2，1，3）为法向量的平面的方程为（ ）μ发布：2024/10/23 6:0:3组卷：89引用：4难度：0.8 -
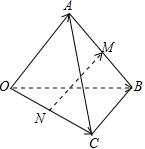2．三棱锥O-ABC中，M，N分别是AB，OC的中点，且=OA，a=OB，b=OC，用c，a，b表示c，则NM等于（ ）NM发布：2024/12/17 2:30:1组卷：2291引用：19难度：0.9 -
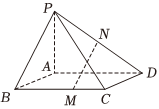3．四棱锥P-ABCD底面ABCD为平行四边形，M，N分别为棱BC，PD上的点，，PN=ND，设CMCB=13，AB=a，AD=b，则向量AP=c用基底MN表示为（ ）{a，b，c}
发布：2024/10/25 4:0:2组卷：433引用：6难度：0.7
