如图，将边长为（a+b）的正方形剪出两个边长分别为a,b的正方形（阴影部分）．
观察图形，解答下列问题：
（1）根据题意，用两种不同的方法表示阴影部分的面积，即用两个不同的代数式表示阴影部分的面积．方法1：a2+b2a2+b2，方法2：（a+b）2-2ab（a+b）2-2ab；
（2）从（1）中你能得到怎样的等式？a2+b2=（a+b）2-2aba2+b2=（a+b）2-2ab；
（3）运用你发现的结论，解决下列问题：
①已知x+y=5，12xy=2，求x2+y2的值；
②已知（2023-x）2+（x-2022）2=15，求（2023-x）（x-2022）的值．
1
2
xy
=
2
【考点】完全平方公式的几何背景；多项式乘多项式．
【答案】a2+b2；（a+b）2-2ab；a2+b2=（a+b）2-2ab
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/11 8:0:9组卷：104引用：1难度：0.6
相似题
-
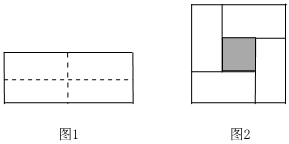1．学完整式的乘法公式后，爱思考的小丽同学为了探究公式之间的联系，她把一个长为2a,宽为2b的长方形沿图1中虚线用剪刀平均分成四个小长方形，然后拼成一个大正方形（如图2）．请你根据小丽的操作回答下列问题：
（1）图1中每个小长方形的长和宽分别为 ，图2中大正方形的边长为 ，中间小正方形（阴影部分）的边长为 （均用含a,b的式子表示）；
（2）小丽发现可以用两种方法求图2中小正方形（阴影部分）的面积，请你帮她写出来（直接用含a,b的式子表示，不必化简）：方法1：，方法2：．
（3）根据（2）中的结论，探究（a+b）2，（a-b）2，ab间的等量关系．发布：2025/6/8 15:30:1组卷：50引用：1难度：0.5 -
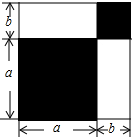2．请认真观察图形，解答下列问题：
（1）根据图中条件，用两种方法表示两个阴影图形的面积的和（只需表示，不必化简）；
（2）由（1），你能得到怎样的等量关系？请用等式表示；
（3）如果图中的a,b（a＞b）满足a2+b2=53，ab=14，求：
①a+b的值；
②a4-b4的值．发布：2025/6/8 16:0:1组卷：4800引用：21难度：0.3 -
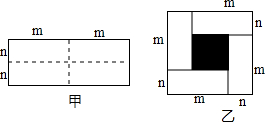3．已知图甲是一个长为2m,宽为2n的长方形，沿图中虚线用剪刀均剪成四个小长方形，然后拼成如图乙所示的一个大正方形．
（1）你认为图乙中的阴影部分的正方形的边长=；
（2）请用两种不同的方法求图乙中阴影部分的面积：
方法一：
方法二：
（3）观察图乙，请你写出下列代数式之间的等量关系：
（m+n）2、（m-n）2、mn
．
（4）根据（3）题中的等量关系，解决如下问题：若a+b=8，ab=7，求a-b的值．发布：2025/6/8 14:30:2组卷：702引用：3难度：0.5
