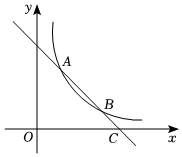
如图，一次函数y=-x+3的图象与反比例函数y=kx（k≠0）在第一象限的图象交于A（1，a）和B（2，b）两点，与x轴交于点C．
（1）求反比例函数的关系式；
（2）根据图象，当-x+3＜kx时x的取值范围为：0＜x＜1或x＞20＜x＜1或x＞2；
（3）若点P在x轴上，且S△APC=103S△AOB，求点P的坐标；
（4）若点P在y轴上，Q在双曲线上，当以A、B、P、Q为顶点的四边形是平行四边形时，直接写出Q点的坐标：）（3，23）或（-1，-2））（3，23）或（-1，-2）．
y
=
k
x
（
k
≠
0
）
-
x
+
3
＜
k
x
S
△
APC
=
10
3
S
△
AOB
（
3
，
2
3
）
（
3
，
2
3
）
【考点】反比例函数综合题．
【答案】0＜x＜1或x＞2；）或（-1，-2）
（
3
，
2
3
）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/20 8:0:8组卷：1399引用：5难度：0.5
相似题
-
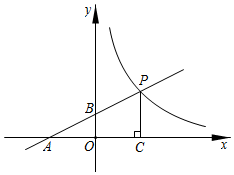1．如图，直线y=ax+1与x轴、y轴分别相交于A、B两点，与双曲线y=（x＞0）相交于点P，PC⊥x轴于点C，且PC=2，点A的坐标为（-2，0）．kx
（1）求直线AP和双曲线的解析式；
（2）若点Q为双曲线上点P右侧的一点，且QH⊥x轴于H，当以点Q、C、H为顶点的三角形与△AOB相似时，求点Q的坐标．发布：2025/5/24 15:0:1组卷：1394引用：12难度：0.3 -
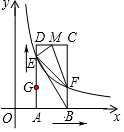2．如图，在平面直角坐标系第一象限中，已知点A坐标为（1，0），点D坐标为（1，3），点G坐标为（1，1），动点E从点G出发，以每秒1个单位长度的速度匀速向点D方向运动，与此同时，x轴上动点B从点A出发，以相同的速度向右运动，两动点运动时间为t（0＜t＜2），以AD、AB分别为边作矩形ABCD，过点E作双曲线交线段BC于点F，作CD中点M，连接BE、EF、EM、FM．
（1）当t=1时，求点F的坐标．
（2）若BE平分∠AEF，则t的值为多少？
（3）若∠EMF为直角，则t的值为多少？发布：2025/5/24 14:30:1组卷：1028引用：5难度：0.3 -
3．两个反比例函数和y=kx在第一象限内的图象如图所示，点P在y=1x的图象上，PC⊥x轴于点C，交y=kx的图象于点A，PD⊥y轴于点D，交y=1x的图象于点B，当点P在y=1x的图象上运动时，以下结论：y=kx
①△ODB与△OCA的面积相等；
②四边形PAOB的面积不会发生变化；
③PA与PB始终相等；
④当点A是PC的中点时，点B一定是PD的中点．
其中，正确的结论有（ ）发布：2025/5/24 16:0:1组卷：1059引用：8难度：0.7
