数学课上，老师准备了三种纸片，如图1中边长分别为a、b的正方形纸片A、B，以及长为b、宽为a的长方形纸片C，观察图形并解答下列问题：
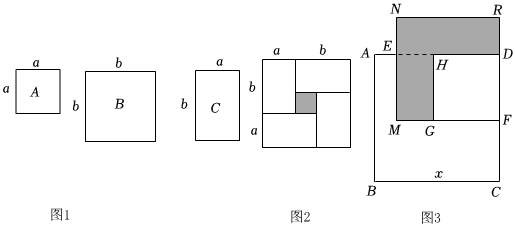
（1）小玲想用图1的三种纸片拼出一个面积为（3a+b）（a+b）的大长方形，则需要A纸片 33张，B纸片 11张，C纸片 44张（空格处填写数字）．
（2）观察图2，请写出下列三个代数式（b+a）2，（b-a）2，ab之间的等量关系：（b+a）2=（b-a）2+4ab（b+a）2=（b-a）2+4ab．
（3）根据（2）中的关系，若m满足（2-m）（m-5）=1，求m的值．
（4）已知正方形ABCD的边长为x,E，F分别是AD、DC上的点，且AE=1，CF=3，长方形EMFD的面积是8，分别以MF、DF为边作正方形，求阴影部分的面积．
【考点】完全平方公式的几何背景；多项式乘多项式．
【答案】3；1；4；（b+a）2=（b-a）2+4ab
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/21 11:0:12组卷：237引用：2难度：0.5
相似题
-
1．已知x2+4y2=13，xy=3，求x+2y的值，这个问题我们可以用边长分别为x和y的两种正方形组成一个图形来解决，其中x＞y,能较为简单地解决这个问题的图形是（ ）
发布：2025/6/22 15:30:1组卷：2384引用：20难度：0.7 -
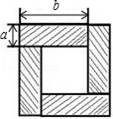2．如图是用4个全等的长方形拼成的一个“回形”正方形，将图中阴影部分面积用2种方法表示可得一个等式，这个等式为．发布：2025/6/23 19:0:1组卷：340引用：3难度：0.7 -
3．图1是一个长为2a,宽为2b的长方形，沿图中虚线剪开分成四块小长方形，然后按图2 的形状拼成一个正方形．
（1）图2的阴影部分的正方形的边长是．
（2）用两种不同的方法求图中阴影部分的面积．
【方法1】S阴影=；
【方法2】S阴影=；
（3）观察图2，写出（a+b）2，（a-b）2，ab 这三个代数式之间的等量关系．
（4）根据（3）题中的等量关系，解决问题：若m+n=10，m-n=6，求mn的值．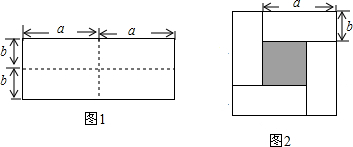
发布：2025/6/24 1:30:2组卷：1437引用：10难度：0.3
