已知△ABC和△ADE都是等边三角形．
【模型感知】（1）如图1，求证：BE=CD；
【模型应用】（2）如图2，当点D在CB的延长线上时，求证：AB+BD=BE；
【类比探究】（3）如图3，当点D在射线BC上时，过点E作EF⊥AB于点F．猜想线段AB，BF与BD之间存在的数量关系，并证明你的猜想．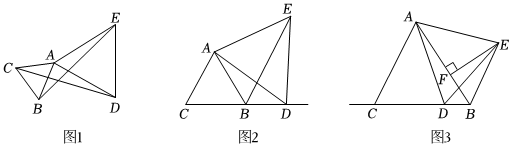
【考点】旋转的性质；全等三角形的判定与性质．
【答案】（1）答案见解答过程；
（2）答案见解答过程；
（3）AB=BD+2BF，证明见解答过程．
（2）答案见解答过程；
（3）AB=BD+2BF，证明见解答过程．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/23 6:0:3组卷：861引用：4难度：0.5
相似题
-
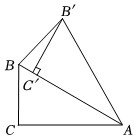1．如图，Rt△ABC中，∠BAC=40°，∠C=90°，将△ABC绕点A旋转，使得点C的对应点C′落在AB上，则∠BB′C′的度数为（ ）发布：2025/6/19 22:30:1组卷：49引用：2难度：0.7 -
2．如图，将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′，若∠AOB=25°，则∠AOB′的度数是（ ）发布：2025/6/19 22:0:1组卷：682引用：11难度：0.8 -
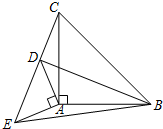3．如图，在△ABC与△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C、D、E在同一条直线上，连接BD、BE．把以下所有正确结论的序号都填在写在横线上：．
①BD=CE；②CD=DE；③BD⊥CE．发布：2025/6/19 22:30:1组卷：30引用：1难度：0.6
