解答下列问题:
(1)【问题呈现】阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,点M是ˆABC的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=DB+BA.下面是运用“截长法”证明CD=DB+BA的部分证明过程.
证明:如图2,在CD上截取CG=AB,连接MA、MB、MC和MG.
∵M是ˆABC的中点,∴ˆMA=ˆMC,
∴MA=MC①,
又∵∠A=∠C②,
∴△MAB≌△MCG,
∴MB=MG,
又∵MD⊥BC,
∴BD=DG,
∴AB+BD=CG+DG,
即CD=DB+BA,
根据证明过程,分别写出下列步骤的理由:
①相等的弧所对的弦相等相等的弧所对的弦相等,
②同弧所对的圆周角相等同弧所对的圆周角相等.
(2)【理解运用】如图1,AB、BC是⊙O的两条弦,AB=8,BC=12,点M是ˆABC的中点,MD⊥BC于点D,则BD的长为 22.
(3)【变式探究】如图3,若点M是ˆAC的中点,【问题呈现】中的其他条件不变,判断CD、DB、BA之间存在怎样的数量关系?并加以证明.
(4)【实践应用】根据你对阿基米德折弦定理的理解完成下列问题:
如图4,BC是⊙O的直径,点A圆上一定点,点D圆上一动点,且满足∠DAC=45°,若AB=12,⊙O的半径为10,求AD长.

ˆ
ABC
ˆ
ABC
ˆ
MA
ˆ
MC
ˆ
ABC
ˆ
AC
【考点】圆的综合题.
【答案】相等的弧所对的弦相等;同弧所对的圆周角相等;2
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/21 20:0:1组卷:342引用:2难度:0.2
相似题
-
1.在⊙O中,直径AB与弦CD(非直径)交于点E,DE=CE,弦BG⊥BC交⊙O于点G,交CD于点F.
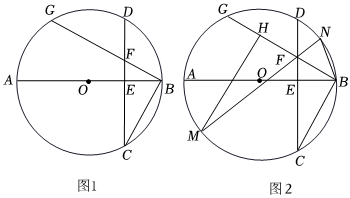
(1)如图1,求证:∠ABF=∠BCD;
(2)如图2,点N为弧BD上一点,连接BN、NF,并延长NF交⊙O于点M,H为FG上一点,连接MH,BN=BF,∠HMF=∠HBN,求证:FH=GH.12发布:2025/5/24 14:30:1组卷:107引用:1难度:0.1 -
2.如图1,在Rt△ABC中,∠ABC=90°,以线段BC为直径作⊙O交AC于点D,E为AB中点,连接ED,过点C作CF∥AB交ED的延长线于点F.
(1)求证:直线ED是⊙O的切线;
(2)判断△CDF的形状,并说明理由;
(3)如图2,连接OF交⊙O于点P,连接BP交AC于点Q,若D为AQ中点,AB=6,求PQ的长.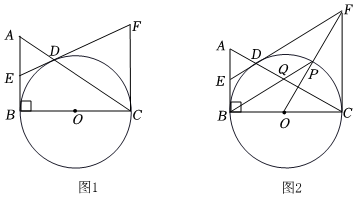 发布:2025/5/24 13:30:2组卷:319引用:2难度:0.3
发布:2025/5/24 13:30:2组卷:319引用:2难度:0.3 -
3.已知在Rt△ABC中,∠C=90°,AC=
,BC=2.23
(1)如图①,若P为BC上由点B向点C运动的一点,连接AP,设AP的中点为G,求在点P运动的过程中,点G经过的路径长.
(2)如图②,若P是以AB为直径所作半圆上由点A沿着半圆向点B运动的一点,求CP的中点F经过的路径长.
(3)如图③,若P为BC上由点B向点C运动的一点,连接AP,作BR⊥AP于点R,(P、R可以重合)求在点P的运动过程中,R经过的路径长.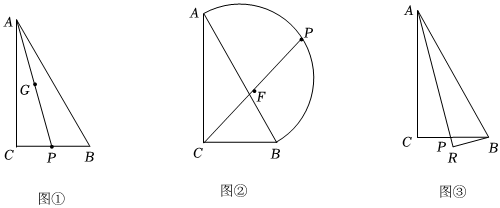 发布:2025/5/24 13:30:2组卷:86引用:1难度:0.3
发布:2025/5/24 13:30:2组卷:86引用:1难度:0.3


