问题提出：（1）如图①，在等腰Rt△ABC中，∠ACB=90°，D是AB边上一点，以CD为腰作等腰Rt△CDE，连接BE，则AD与BE的数量关系是 相等相等，位置关系是 垂直垂直；
问题探究：（2）如图②，AB是半圆O的直径，C、D是半圆O上两点，且AC=BC，若BD=3，AD=9，求CD的长；
问题解决：（3）如图③是某公园的一个面积为36πm2的圆形广场示意图，点O为圆心，公园开发部门计划在该广场内设计一个四边形运动区域ABDC，连接BC，AD，其中等边△ABC为球类运动区域，△BCD为散步区域，按照设计要求，发现当点D为ˆBC的中点时，布局设计最佳，求此时四边形运动区域ABDC的面积．
ˆ
BC
【考点】圆的综合题．
【答案】相等；垂直
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/21 8:0:9组卷：159引用：2难度：0.1
相似题
-
1．直角三角板ABC的斜边AB的两个端点在⊙O上，已知∠BAC=30°，直角边AC与⊙O相交于点D，且点D是劣弧AB的中点．
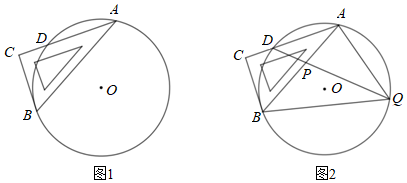
（1）如图1，判断直角边BC所在直线与⊙O的位置关系，并说明理由；
（2）如图2，点P是斜边AB上的一个动点（与A、B不重合），DP的延长线交⊙O于点Q，连接QA、QB．
①AD=6，PD=4，则AB=；PQ=；
②当点P在斜边AB上运动时，求证：QA+QB=QD．3发布：2025/5/25 5:30:2组卷：139引用：3难度：0.3 -
2．如果一个四边形的对角线相等，我们称这个四边形为美好四边形．
【问题提出】
（1）如图①，点E是四边形ABCD内部一点，且满足EB=EC，EA=ED，∠BEC=∠AED，请说明四边形ABCD是美好四边形；
【问题探究】
（2）如图②，△ABC，请利用尺规作图，在平面内作出点D使得四边形ABCD是美好四边形，且满足AD=BD．保留作图痕迹，不写画法；
（3）在（2）的条件下，若图②中△ABC满足：∠ABC=90°，AB=4，BC=3，求四边形ABCD的面积；
【问题解决】
（4）如图③，某公园内需要将4个信号塔分别建在A、B、C、D四处，现要求信号塔C建在公园内一个湖泊的边上，该湖泊可近似看成一个半径为200m的圆，记为⊙E．已知点A到该湖泊的最近距离为500m,是否存在这样的点D，满足AC=BD，且使得四边形ABCD的面积最大？若存在，求出最大值；若不存在，请说明理由．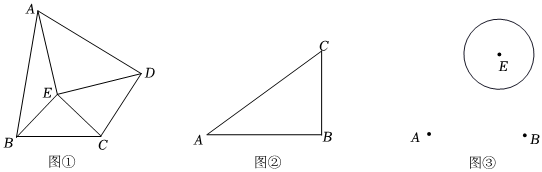
发布：2025/5/25 3:30:2组卷：216引用：2难度：0.1 -
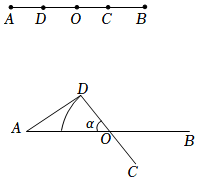3．如图1，在一平面内，从左到右，点A，D，O，C，B均在同一直线上．线段AB=20，线段CD=10，O是AB，CD的中点．固定点O以及线段AB，让线段CD绕点O顺时针旋转α（0°＜α＜180°）．
（1）连接AC，AD，BC，BD．
①求证：四边形ADBC为平行四边形；
②当α=90°时，求四边形ADBC的周长；
（2）连接AD．某个时刻，直线AD与线段OD旋转形成的扇形相切于点D，如图2所示，求此时线段OD扫过的扇形面积．发布：2025/5/25 6:0:1组卷：77引用：2难度：0.4
