如图，以点B为圆心以任意长为半径画弧，分别交∠ABC的两边BA、BC于点D、E，分别以D、E为圆心以DE的长为半径画弧，两弧相交于点F，作射线BF，过点F作FG∥AB交BC于点G．若射线BA上存在点M，使FM=FG，则当∠ABC=40°时，∠FMB的度数是（ ）
【答案】D
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：52引用：1难度：0.5
相似题
-
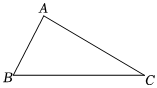1．如图，已知△ABC，以点B为圆心，AC长为半径画弧；以点C为圆心，AB长为半径画弧，两弧交于点D，且点A，点D在BC异侧，连接AD，量一量线段AD的长，约为（ ）发布：2025/6/19 21:0:2组卷：413引用：40难度：0.5 -
2．如图，已知△ABC．
（1）作中线AD；
（2）尺规作出角平分线BE；
（3）作BC边的高线．发布：2025/6/20 0:0:1组卷：114引用：2难度：0.5 -
3．下面是小雅同学设计的“作已知圆的内接正三角形”的尺规作图过程．
已知：⊙O．
求作：⊙O的内接正三角形ABC．
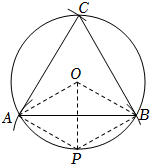
作法：如图，①在⊙O上取任意一点P，以点P为圆心，OP长为半径作弧，交⊙O于A、B两点；
②以A为圆心，AB长为半径作弧，与⊙O交于点C；
③连接AB，BC，AC．
所以△ABC就是所求的三角形．
请你根据小雅同学设计的尺规作图过程，完成证明过程：
连接OA、OB、OP、PA、PB，
∵OA=OB=OP=PA=PB，
∴△OPA和△OPB是 ，
∴∠AOB=∠AOP+∠BOP=120°，
∵，ˆAB=ˆAB
∴（ ）（填推理依据），∠ACB=12∠AOB=60°
∵AB=，
∴△ABC是等边三角形．发布：2025/6/20 0:0:1组卷：39引用：1难度：0.6
