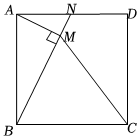
如图，正方形ABCD的边长为4，N为AD上一点，连接BN，AM⊥BN于点M，连接CM，若AM=2，则△BCM的面积为（ ）
【考点】正方形的性质；全等三角形的判定与性质．
【答案】B
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/15 8:0:8组卷：493引用：2难度：0.5
相似题
-
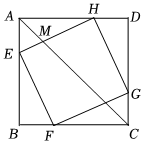1．如图，点E，F，G，H分别位于正方形ABCD的四条边上（AE＜AH），四边形EFGH也是正方形，连接AC交EH于点M，设∠AHE=α，若MC=4AM，则tanα的值为 ．发布：2025/5/23 16:0:1组卷：203引用：1难度：0.4 -
2．如图，点E在正方形ABCD的边BC上，连接DE、BD，延长CB到点F，使BF=CE，过点E作EG⊥BD于点G，连接FG．若DE=4，则FG的长为 ．3发布：2025/5/23 15:0:2组卷：952引用：3难度：0.2 -
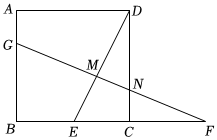3．在正方形ABCD中，E是BC边上一点，在BC延长线上取点F使EF=ED．过点F作FG⊥ED交ED于点M，交AB于点G．交CD于点N．
（1）求证：△CDE≌△MFE；
（2）若E是BC的中点，请判断BG与MG的数量关系．并说明理由．发布：2025/5/23 16:0:1组卷：638引用：3难度：0.6
