阅读理解并回答问题.观察下列算式:
16=12×3=12-13; 112=13×4=13-14; 120=14×5=14-15; ……
(1)填空:142=16×716×7=16-1716-17;
(2)请用含有m(m表示整数)的代数式表示上述式子特点的一般规律:1m(m+1)=1m-1m+11m(m+1)=1m-1m+1.
(3)请用(2)中的规律解方程:1x ( x+1)+1( x+1 )( x+2 )+…+1( x+9 )( x+10 )=1( x+10 ).
1 6 = 1 2 × 3 = 1 2 - 1 3 ; |
1 12 = 1 3 × 4 = 1 3 - 1 4 ; |
1 20 = 1 4 × 5 = 1 4 - 1 5 ; |
…… |
1
42
1
6
×
7
1
6
×
7
1
6
1
7
1
6
1
7
1
m
(
m
+
1
)
=
1
m
-
1
m
+
1
1
m
(
m
+
1
)
=
1
m
-
1
m
+
1
1
x
(
x
+
1
)
+
1
(
x
+
1
)
(
x
+
2
)
+
…
+
1
(
x
+
9
)
(
x
+
10
)
=
1
(
x
+
10
)
【答案】;-;
1
6
×
7
1
6
1
7
1
m
(
m
+
1
)
=
1
m
-
1
m
+
1
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/7/10 8:0:8组卷:111引用:5难度:0.7
相似题
-
1.观察下列各式:
,11×3=12×(1-13),13×5=12×(13-15),…,15×7=12×(15-17),…199×101=12×(199-1101)
计算下列各题:;(1)11×3+13×5+15×7+⋯+199×101.(2)12×6+16×10+110×14+⋯+12018×2022发布:2025/6/8 22:30:1组卷:84引用:1难度:0.6 -
2.已知n≥2,且n为自然数,对n2进行如下“分裂”,可分裂成n个连续奇数的和,如图:
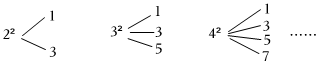
即如下规律:22=1+3,32=1+3+5,42=1+3+5+7,……
(1)按上述分裂要求,将5分裂成奇数和的形式:52=;102可分裂的最大奇数为 ;
(2)按上述分裂要求,n2可分裂成连续奇数和的形式是:n2=1+3+5+…+(填最大奇数,用含n的式子表示);
(3)用上面的规律求:(n+1)2-n2.发布:2025/6/9 0:0:2组卷:111引用:4难度:0.5 -
3.按一定规律排列的单项式:a,-2a,4a,-8a,16a,-32a,64a,…,第2021个单项式是 .
发布:2025/6/8 21:0:2组卷:236引用:3难度:0.5


