定义:若两个椭圆的离心率相等,则称这两个椭圆相似.如图,椭圆C1、C2是两个相似的椭圆,椭圆C1:x2a2+y2b2=1(a>b>0)的长半轴长是4,短半轴长是2,且C1的左、右焦点F1、F2都在椭圆C2:x2m2+y2n2=1(m>n>0)上.
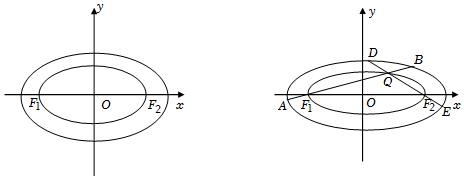
(1)求C1、C2的方程;
(2)在C1上是否存在点P满足,线段PF1的中点在C2上,如有请求出P的坐标,否则请说明理由;
(3)如图,若Q是C2上异于F1、F2的任意一点,直线QF1与C1交于A、B两点,直线QF2与C1交于D、E两点,求证:|AB|+|DE|为定值.
x
2
a
2
+
y
2
b
2
x
2
m
2
+
y
2
n
2
【考点】直线与圆锥曲线的综合.
【答案】(1),;(2)存在,;(3)10.
C
1
:
x
2
16
+
y
2
4
=
1
C
2
:
x
2
12
+
y
2
3
=
1
P
(
-
17
3
3
,
±
69
6
)
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/27 10:35:59组卷:187引用:2难度:0.3
相似题
-
1.已知两个定点坐标分别是F1(-3,0),F2(3,0),曲线C上一点任意一点到两定点的距离之差的绝对值等于2
.5
(1)求曲线C的方程;
(2)过F1(-3,0)引一条倾斜角为45°的直线与曲线C相交于A、B两点,求△ABF2的面积.发布:2024/12/29 10:30:1组卷:101引用:1难度:0.9 -
2.点P在以F1,F2为焦点的双曲线
(a>0,b>0)上,已知PF1⊥PF2,|PF1|=2|PF2|,O为坐标原点.E:x2a2-y2b2=1
(Ⅰ)求双曲线的离心率e;
(Ⅱ)过点P作直线分别与双曲线渐近线相交于P1,P2两点,且,OP1•OP2=-274,求双曲线E的方程;2PP1+PP2=0
(Ⅲ)若过点Q(m,0)(m为非零常数)的直线l与(2)中双曲线E相交于不同于双曲线顶点的两点M、N,且(λ为非零常数),问在x轴上是否存在定点G,使MQ=λQN?若存在,求出所有这种定点G的坐标;若不存在,请说明理由.F1F2⊥(GM-λGN)发布:2024/12/29 10:0:1组卷:72引用:5难度:0.7 -
3.若过点(0,-1)的直线l与抛物线y2=2x有且只有一个交点,则这样的直线有( )条.
发布:2024/12/29 10:30:1组卷:26引用:5难度:0.7


