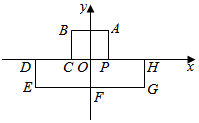
如图，在平面直角坐标系中，AB∥EG∥x轴，BC∥DE∥HG∥AP∥y轴，点D、C、P、H在x轴上，A（1，2），B（-1，2），D（-3，0），E（-3，-2），G（3，-2），把一条长为2019个单位长度且没有弹性的细线（粗细忽略不计）的一端固定在点A处，并按A-B-C-D-E-F-G-H-P-A…的规律紧绕在图形“凸”的边上，则细线另一端所在位置的点的坐标是（　　）

A．（1，2）

B．（-1，2）

C．（-1，-2）

D．（1，1）

【答案】D

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/5/27 14:0:0组卷：345引用：4难度：0.6

相似题

1．在平面直角坐标系中，对于点P（x,y），我们把点P′（1-y,x-1）叫做点P的友好点，已知点A₁的友好点为A₂，点A₂的友好点为A₃，点A₃的友好点为A₄，…，这样依次得到点A₁，A₂，A₃，A₄，…，若点A₁的坐标为（2，1），则点A₂₀₂₂的坐标为（　　）
A．（2，1） B．（0，1） C．（0，-1） D．（2，-1）
发布：2025/6/8 9:30:1组卷：59引用：1难度：0.6
解析
2．在平面直角坐标系xOy中，对于点P（x,y）我们把点P（-y+1，x+1）叫做点P的伴随点．已知点A₁的伴随点为A₂，点A₂的伴随点为A₃，点A₃的伴随点为A₄，…这样依次得到点A₁，A₂，A₃，…，A_n，…．若点A₁的坐标为（2，4），点A₂₀₂₂的坐标为（　　）
A．（-3，3） B．（-2，-2） C．（3，-1） D．（2，4）
发布：2025/6/8 7:30:1组卷：163引用：1难度：0.5
解析
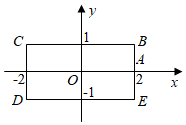3．如图，长方形BCDE的各边分别平行于x轴与y轴，物体甲和物体乙由点A（2，0）同时出发，沿长方形BCDE的边做环绕运动，物体甲按逆时针方向以1个单位长度/秒的速度匀速运动，物体乙按顺时针方向以2个单位长度/秒的速度匀速运动，则两个物体运动后的第2022次相遇地点的坐标是（　　）
A．（1，-1） B．（-1，-1） C．（-1，1） D．（2，0）
发布：2025/6/8 8:0:6组卷：328引用：5难度：0.6
解析