高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的美誉，用其名字命名的“高斯函数”为：设x∈R，用[x]表示不超过x的最大整数，则y=[x]称为高斯函数．如[-2.9]=-3
，[3.5]=3，令f（x）=[x]．
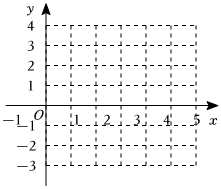
（1）记h（x）=2f（x）-x,x∈[0，3），求h（x）的解析式，并在坐标系中作出函数h（x）的图象；
（2）结合（1）中的图象，解不等式12＜h（x）≤54直接写出结果；
（3）设g（x）=3x-13x+1，判断g（x）的奇偶性，并求函数y=2f（g（x））+f（g（-x））的值域．
[ - 2 . 9 ] = - 3 |
1
2
＜
h
（
x
）
≤
5
4
g
（
x
）
=
3
x
-
1
3
x
+
1
【答案】（1）h（x）=
，图象见解析；
（2）或；
（3）{-1，-2，0}，奇函数．
- x ， 0 ≤ x ＜ 1 |
2 - x ， 1 ≤ x ＜ 2 |
4 - x ， 2 ≤ x ＜ 3 |
（2）
{
x
|
1
≤
x
＜
3
2
11
4
＜
x
＜
3
}
（3）{-1，-2，0}，奇函数．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/11 8:0:9组卷：43引用：2难度：0.5
