如图①，AB是⊙O的直径，AB=8，点C在⊙O上且位于直线AB上方，将半径OC绕点O顺时针旋转40°，点C的对应点为点D，连结CD，BD．
（1）以CD为边的⊙O内接正多边形的边数为 99；
（2）当直径AB平分∠COD时，求ˆAC 的长；
（3）连结BC，当tan∠BCD=34 时，求BD的长；
（4）如图②，连结AC并延长，交BD的延长线于点E，当△ABE是等腰三角形时，直接写出扇形AOD的面积．
ˆ
AC
tan
∠
BCD
=
3
4
【考点】圆的综合题．
【答案】9
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/8 8:0:9组卷：169引用：1难度：0.5
相似题
-
1．如图，锐角△ABC中∠A的平分线交BC于点E，交△ABC的外接圆于点D、边BC的中点为M．
（1）求证：MD垂直BC；
（2）若AC=5，BC=6，AB=7．求的值；BDAD
（3）作∠ACB的平分线交AD于点P，若将线段MP绕点M旋转180°后，点P恰好与△ABC外接圆上的点P'重合，则tan∠BAC=．发布：2025/5/24 3:30:1组卷：447引用：3难度：0.3 -
2．【概念学习】
在平面直角坐标系xOy中，⊙O的半径为1，若⊙O平移d个单位后，使某图形上所有点在⊙O内或⊙O上，则称d的最小值为⊙O对该图形的“最近覆盖距离”．例如，如图①，A（3，0），B（4，0），则⊙O对线段AB的“最近覆盖距离”为3．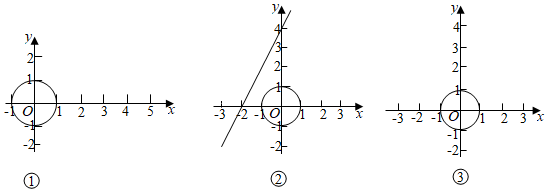
【概念理解】
（1）⊙O对点（3，4）的“最近覆盖距离”为 ．
（2）如图②，点P是函数y=2x+4图象上一点，且⊙O对点P的“最近覆盖距离”为3，则点P的坐标为 ．
【拓展应用】
（3）如图③，若一次函数y=kx+4的图象上存在点C，使⊙O对点C的“最近覆盖距离”为1，求k的取值范围．
（4）D（3，m）、E（4，m+1），且-4＜m＜2，将⊙O对线段DE的“最近覆盖距离”记为d,则d的取值范围是 ．发布：2025/5/24 4:0:7组卷：1245引用：3难度：0.3 -
3．【问题提出】
（1）如图①，已知在四边形ABCD中，AD∥BC，对角线AC与BD相交于点O，则S△AOBS△COD（填“＞”“＜”或“=”）．
【问题探究】
（2）如图②，在Rt△ABC中，AB=4，AC=3，∠BAC=90°，点E、点F分别为BC、AC边上的两个点，连接AE、EF，过点F作FD∥AE，交BC于点D，连接AD，若EF恰好将△ABC分为面积相等的两部分，求AD的长．
【问题解决】
（3）杨叔叔承包了一块土地欲进行耕种，土地形状如图③所示，其中四边形ABCD的面积为12600平方米，AB∥CD，AB=160米，CD=120米，tanB=，1817所在圆的半径为65米．已知ˆCD的中点P处有一口灌溉水井，现结合实际耕种需求，需在AB上找一点Q，使PQ将这块土地的面积分为相等的两部分，用于耕种两种不同的作物，并沿PQ修一条灌溉水渠（水渠的宽度忽略不计），请在图中找出点Q的位置，并计算灌溉水渠PQ的长．（结果保留根号）ˆCD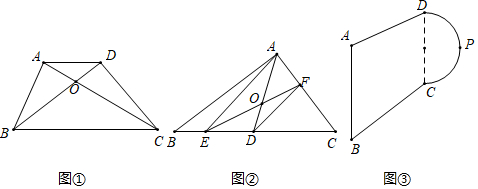
发布：2025/5/24 2:30:1组卷：622引用：2难度：0.2
