在正方形ABCD中，点E是对角线AC上的一点，且AE=1nAC（n＞2），将线段AE绕着点E顺时针旋转至EF，记旋转角为α（0＜α≤180°），连接AF、CF，并以CF为斜边在其上方作△CFG∽△CAD，连接DG．
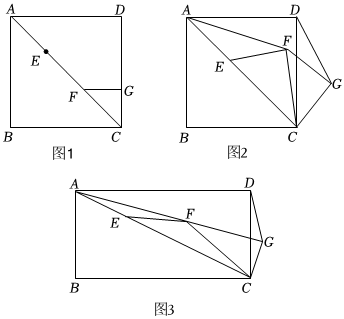
（1）特例探究：如图1，当n=3，α=180°时，线段AF与DG的数量关系为 AF=2DGAF=2DG；
（2）问题探究：如图2所示，在旋转的过程中，
①（1）中的结论是否依然成立，若成立，请说明理由；
②当n=83，∠EFC=90° 时，若AB=42，求DG的长度；
（3）拓展提升：若正方形ABCD改为矩形ABCD，且ABAD=12，其它条件不变，在旋转的过程中，当A、F、G三点共线时，如图3所示，若n=4，CG=m,直接写出DG的长度．（用含m的式子表示）
AE
=
1
n
AC
（
n
＞
2
）
2
2
n
=
8
3
AB
=
4
2
AB
AD
=
1
2
【考点】相似形综合题．
【答案】AF=DG
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：972引用：2难度：0.3
相似题
-
1．如图1，在Rt△ABC中，∠BAC=90°，D为边AB上一点，∠ACD=∠B．
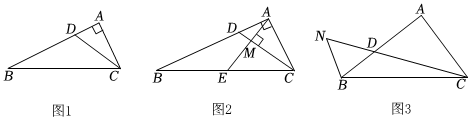
（1）求证：AC2=AD•AB；
（2）如图2，过点A作AM⊥CD于M，交BC于点E，若AB=4AD，求的值；AMME
（3）如图，N为CD延长线上一点，连接BN，且∠NBD=2∠ACD，若，直接写出tan∠ACD=1n（n＞1）的值（用含n的代数式表示）．NDDC发布：2025/5/22 10:30:1组卷：557引用：4难度：0.1 -
2．问题背景：某学习小组正在研究如下问题：如图1所示，四边形ABCD与四边形CEFG均为正方形，且点E、G分别在边BC、CD上，连接DE、BG，点M是BG中点，连接CM，试猜测CM与DE的数量关系与位置关系，并加以证明．
解决问题：小华从旋转的角度提出一个问题：如图2，将正方形CEFG绕点C顺时针旋转一定角度，其他条件不变，此时“问题背景”中的结论还成立吗？如果成立，请加以证明；如果不成立，请说明理由．
拓展延伸：小刚提出了一个更加一般化的问题：如图3所示，▱ABCD∽▱ECGF，且，其他条件不变，此时CM与DE又有怎样的数量关系？请直接写出结果．ABBC=ab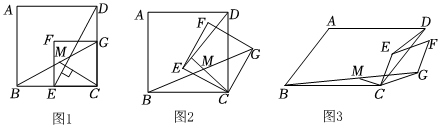
发布：2025/5/22 10:30:1组卷：242引用：4难度：0.1 -
3．如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=3．点D是边AC上一动点（不与A、C重合），联结BD，过点C作CF⊥BD，分别交BD、AB于点E、F．
（1）当CD=2时，求∠ACF的正切值；
（2）设CD=x,，求y关于x的函数解析式，并写出x的定义域；AFBF=y
（3）联结FD并延长，与边BC的延长线相交于点G，若△DGC与△BAC相似，求的值．AFBF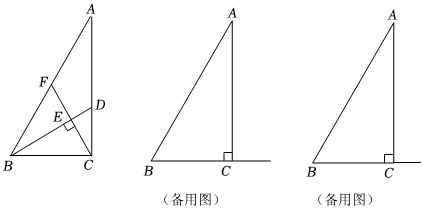
发布：2025/5/22 11:30:2组卷：530引用：1难度：0.4
