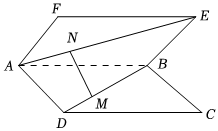
如图，在矩形ABCD和ABEF中，AB=4，AD=AF=3，∠DAF=π3，DM=λDB，AN=λAE，0＜λ＜1，记AB=a，AD=b，AF=c．
（1）将MN用a，b，c表示出来，并求|MN|的最小值；
（2）是否存在λ使得MN⊥平面ABCD？若存在，求出λ的值，若不存在，请说明理由．
∠
DAF
=
π
3
DM
=
λ
DB
AN
=
λ
AE
AB
=
a
，
AD
=
b
，
AF
=
c
MN
a
b
c
|
MN
|
【答案】（1）；
（2）存在，．
3
2
（2）存在，
λ
=
2
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/14 0:0:8组卷：21引用：2难度：0.5
相似题
-
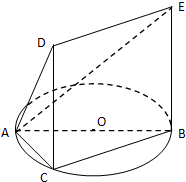1．如图，一简单组合体的一个面ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．
（1）证明：BC⊥平面ACD；
（2）若AB=2，BC=1，tan∠EAB=，试求该简单组合体的体积V．32发布：2025/1/20 8:0:1组卷：25引用：1难度：0.5 -
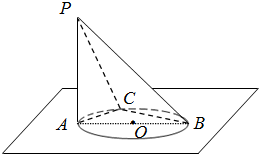2．如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A、B的任意一点．
（1）求证：BC⊥平面PAC；
（2）求证：平面PAC⊥平面PBC．发布：2025/1/28 8:0:2组卷：121引用：3难度：0.3 -
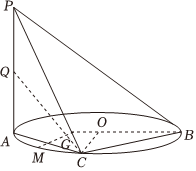3．如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆O上异于A，B的点，
（1）求证：BC⊥平面PAC；
（2）设Q，M分别为PA，AC的中点，问：对于线段OM上的任一点G，是否都有QG∥平面PBC？并说明理由．发布：2025/1/28 8:0:2组卷：34引用：2难度：0.3
