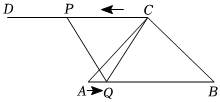
如图，在△ABC中，∠ACB=90°，AC=BC，AB=8cm,过点C作射线CD，且CD∥AB，点P从点C出发，沿射线CD方向匀速运动，速度为3cm/s同时点Q从点A出发，沿AB边向点B匀速运动，速度为1cm/s,当点Q停止运动时，点P也停止运动．连接PQ，CQ，设动点P，Q的运动时间为t（s）（0≤t≤8）．
（1）用含有t的代数式表示CP和BQ的长度，则CP=3t3tcm,BQ=（8-t）（8-t）cm；
（2）当t=2时，试说明PQ∥BC；
（3）设△BCQ的面积为S（cm2），求S与t之间的关系式．
【答案】3t；（8-t）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/14 8:0:9组卷：39引用：1难度：0.5
相似题
-
1．已知：△ABC，∠C=90°，CA=CB，AB=4，点D在AB上，连接CD，CD=
，则BD的长为．5发布：2024/11/5 5:0:3组卷：64引用：3难度：0.6 -
2．两个直角三角板ABC，ADE如图摆放，其中∠BAC=∠DEA=90°，∠B=45°，∠D=60°，若DE∥BC，则∠BAD的大小为（ ）发布：2025/1/1 9:0:3组卷：78引用：2难度：0.7 -
3．如图是一副三角板，其中∠ABC=∠EDF=90°，∠A=45°，∠E=30°，若点B与点F重合，点D在AB边上，AC与EF交于点G，则∠EGC的度数为（ ）发布：2024/11/4 1:30:3组卷：51引用：1难度：0.6
