如图，在平面直角坐标系中，点A在x轴的正半轴上，点B在x轴的负半轴上，点C在y轴的正半轴上，且∠ACB=90°，线段OB、OA的长是一元二次方程x2-13x+36=0的两个根，且OB＜OA．
（1）求点A、点B的坐标；
（2）求点C的坐标；
（3）若直线l过点A交线段BC于点D，且S△ABD：S△ADC=1：2，求D点坐标；
（4）在平面内是否存在一点P，使得以P为直角顶点的△APC与△ABC相似，若存在，请直接写出满足条件的点P的坐标；若不存在，请说明理由．
【考点】相似形综合题．
【答案】（1）A点坐标为（9，0），B点坐标为（-4，0）；
（2）（0，6）；
（3）；
（4）在平面内存在一点P，使得以P为直角顶点的△APC与△ABC相似；（0，0）或或（9，6）或．
（2）（0，6）；
（3）
D
（
-
8
3
，
2
）
（4）在平面内存在一点P，使得以P为直角顶点的△APC与△ABC相似；（0，0）或
（
72
13
，
108
13
）
（
45
13
，-
30
13
）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/2 6:0:2组卷：177引用：6难度：0.1
相似题
-
1．在Rt△ABC中，∠ACB=90°，tan∠ABC=a,D是BC上一点（不与点B，C重合），连接AD，过点C作CE⊥AD于点E，连接BE并延长，交AC于点F．
（1）如图1，当a=1时，
①求证：∠ECD＜45°；
②求证：；BEEF=CDCF
（2）如图2，若D是BC的中点，求tan∠CEF的值（用含a的代数式表示）．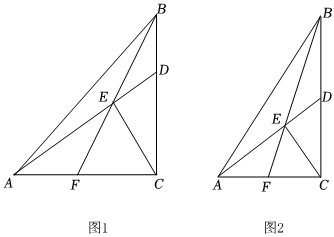
发布：2025/6/5 6:0:2组卷：335引用：4难度：0.3 -
2．综合与实践
我们在没有量角器或三角尺的情况下，用折叠特殊矩形纸片的方法进行如下操作也可以得到几个相似的含有30°角的直角三角形．
实践操作：
第一步：如图①，矩形纸片ABCD的边长AB=，将矩形纸片ABCD对折，使点D与点A重合，点C与点B重合，折痕为EF，然后展开，EF与CA交于点H．5
第二步：如图②，将矩形纸片ABCD沿过点C的直线再次折叠，使CD落在对角线CA上，点D的对应点D'恰好与点H重合，折痕为CG，将矩形纸片展平，连接GH．
问题解决：
（1）在图②中，sin∠ACB=，=；EGCG
（2）在图②中，CH2=CG•；从图②中选择一条线段填在空白处，并证明你的结论；
拓展延伸：
（3）将上面的矩形纸片ABCD沿过点C的直线折叠，点D的对应点D′落在矩形的内部或一边上，设∠DCD′=α，若0°＜α≤90°，连接D′A，D′A的长度为m,则m的取值范围是 ．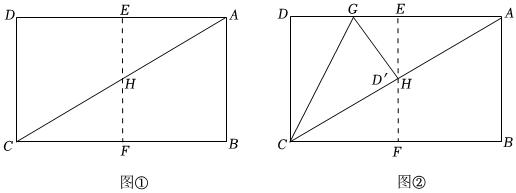
发布：2025/6/5 1:30:2组卷：279引用：2难度：0.2 -
3．（1）如图所示，矩形ABCD中，BC=2AB，将矩形ABCD绕点B逆时针旋转90°，得到新的矩形BEFH，连接FD，EC，线段EC交FD于点G，连BG．
①请直接写出线段FB和BD的数量关系 ，位置关系 ；
②求证：FD=2BG．
（2）如图2所示，Rt△BCD中，∠C=90°，BC=3CD，将Rt△BCD绕点B逆时针旋转α°，得到新的Rt△BEF，连接EC，FD，线段EC，FD相交于点G，点O为线段BD中点，连OG，在Rt△BCD旋转的过程中，是否发生改变？如果不变，请求出OGBC的值；如果发生改变，请说明理由．OGBC发布：2025/6/5 7:30:1组卷：455引用：5难度：0.1
