如图(1)所示,濮阳湿地公园中,金堤河大桥是一座非常有艺术性造型的大桥.桥身是由两条抛物线钢架建造.如图(2)所示,两条抛物线有共同的对称轴,已知y1=-110x2+95x-165,y2过原点,两抛物线最高点的距离为115.
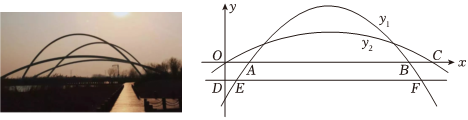
(1)求抛物线y2的解析式;
(2)①求主桥OC长为多少米?
②过点D与x轴平行的直线DF为河面的水平线,OD=32,若要在y1与水面DF的交点E、F处建造两个桥墩,其中一个桥墩E到岸边(y轴)的距离是多少米?(说明:题中1个单位长为50米)
y
1
=
-
1
10
x
2
+
9
5
x
-
16
5
11
5
OD
=
3
2
【考点】二次函数的应用.
【答案】(1)抛物线y2的解析式为;
(2)①主桥OC长为900米;②其中一个桥墩E到岸边(y轴)的距离是50米.
y
2
=
-
1
30
(
x
-
9
)
2
+
27
10
(2)①主桥OC长为900米;②其中一个桥墩E到岸边(y轴)的距离是50米.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/29 8:0:10组卷:86引用:3难度:0.5
相似题
-
1.甲经销商库存有1200套A品牌服装,每套进价400元,每套售价500元,一年内可卖完.现市场上流行B品牌服装,每套进价300元,每套售价600元,但一年内只允许经销商一次性订购B品牌服装,一年内B品牌服装销售无积压.因甲经销商无流动资金,只有低价转让A品牌服装,用转让来的资金购进B品牌服装,并销售.经与乙经销商协商,甲、乙双方达成转让协议,转让价格y(元/套)与转让数量x(套)之间的函数关系式为y=
.若甲经销商转让x套A品牌服装,一年内所获总利润为w(元).-110x+360(100≤x≤1200)
(1)求转让后剩余的A品牌服装的销售款Q1(元)与x(套)之间的函数关系式;
(2)求B品牌服装的销售款Q2(元)与x(套)之间的函数关系式;
(3)求w(元)与x(套)之间的函数关系式,并求w的最大值.发布:2025/5/24 17:0:2组卷:657引用:8难度:0.3 -
2.某超市经销A、B两种商品.商品A每千克成本为20元,经试销发现,该种商品每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价、销售量的对应值如表所示:
商品B的成本为6元/千克,销售单价为10元/千克,但每天供货总量只有60千克,且能当天销售完.为了让利消费者,超市开展了“买一送一”活动,即买1千克的商品A,免费送1千克的商品B.销售单价x(元/千克) 25 30 35 40 销售量y(千克) 50 40 30 20
(1)求y(千克)与x(元/千克)之间的函数表达式;
(2)设这两种商品的每天销售总利润为w元,求出w(元)与x的函数关系式;
(3)若商品A的售价不低于成本,不高于成本的180%,当销售单价定为多少时,才能使当天的销售总利润最大?最大利润是多少?(总利润=两种商品的销售总额-两种商品的成本)发布:2025/5/24 18:0:1组卷:1298引用:8难度:0.4 -
3.已知某商品的进价为每件10元,我班数学兴趣小组经过市场调查,整理出该商品在第x(1≤x≤30)天的售价与销量的相关信息如下表:
(1)第几天该商品的销售单价是25元?第x天 1≤x<15 15≤x≤30 日销售单价(元/千克) 20+ x1210+ 300x日销售量(千克) 40-x
(2)在这30天中,第几天获得的利润最大?最大利润是多少?发布:2025/5/24 18:0:1组卷:172引用:2难度:0.6
相关试卷


