已知双曲线x2a2-y2b2=1，（a＞0，b＞0）的离心率为2，右焦点F到渐近线的距离为3．
（1）求双曲线的标准方程；
（2）若点P为双曲线右支上一动点，过点P与双曲线相切的直线l,直线l与双曲线的渐近线分别交于M，N两点，求△FMN的面积的最小值．
x
2
a
2
-
y
2
b
2
=
1
，
（
a
＞
0
，
b
＞
0
）
3
【考点】双曲线的切线方程及性质．
【答案】1）；
（2）．
x
2
-
y
2
3
=
1
（2）
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/20 7:0:8组卷：135引用：2难度：0.5
相似题
-
1．已知双曲线C：
=1（a＞0，b＞0）上任意一点P（异于顶点）与双曲线两顶点连线的斜率之积为x2a2-y2b2，E在双曲线C上，F为双曲线C的右焦点，|EF|的最小值为2-13．3
（1）求双曲线C的标准方程；
（2）设O为坐标原点，直线l为双曲线C的切线，过F作l的垂线，垂足为A，求证：A在定圆上．发布：2024/6/27 10:35:59组卷：70引用：1难度：0.3 -
2．已知F1，F2分别为双曲线C：
的左、右焦点，点A（x1，y1）为双曲线C在第一象限的右支上一点，以A为切点作双曲线C的切线交x轴于点B，若x2a2-y2b2=1（a＞0，b＞0），且cos∠F1AF2=12，则双曲线C的离心率为（ ）F1B=2BF2发布：2024/10/22 8:0:1组卷：69引用：2难度：0.5 -
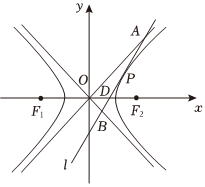3．如图，O为坐标原点，F1，F2分别为双曲线的左、右焦点，过双曲线C右支上一点P作双曲线的切线l分别交两渐近线于A、B两点，交x轴于点D，则下列结论正确的是（ ）C：x2-y2b2=1（b＞0）发布：2024/4/26 11:36:51组卷：229引用：3难度：0.2
