如图,已知女排球场的长度OD为20米,位于球场中线处的球网AB的高度2.24米,一队员站在点O处发球,排球从点O的正上方2米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点O的水平距离OE为6米时,到达最高点G,以O为原点建立如图所示的平面直角坐标系.

(1)写出C点坐标 (0,2)(0,2);B点坐标 (10,2.24)(10,2.24);
(2)若排球运行的最大高度为3米,求排球飞行的高度p(单位:米)与水平距离x(单位:米)之间的函数关系式(不要求写自变量x的取值范围);
(3)在(2)的条件下,这次所发的球能够过网吗?如果能够过网,是否会出界?请说明理由.
【考点】二次函数的应用.
【答案】(0,2);(10,2.24)
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/6 5:0:8组卷:115引用:4难度:0.5
相似题
-
1.孔子曰:温故而知新,可以为师矣.根据艾宾浩斯遗忘曲线,小苏同学发现对所学知识点进行复习回顾,学习效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于学习的时间x(单位:分钟)与学习收益量y的关系如图甲所示,用于复习的时间x(单位:分钟)与学习收益量y的关系如图乙所示(其中OA是抛物线的一部分,A为抛物线的顶点).
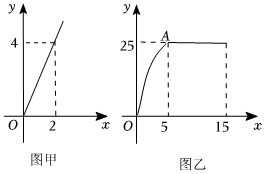
(1)求该同学的学习收益量y与用于学习的时间x之间的函数关系式,并直接写出自变量x的取值范围;
(2)求该同学的学习收益量y与用于复习的时间x之间的函数关系式;
(3)该同学应如何分配学习和复习的时间,才能使这30分钟的学习收益总量最大?(学习收益总量=解题的学习收益量+回顾反思的学习收益量)发布:2025/5/24 20:0:2组卷:170引用:2难度:0.3 -
2.巴中市某中学为增强学生运用数学知识解决实际问题的能力,该校九(1)班同学进行了一次市场调查,收集整理了一种进价每件20元的商品在第x(1≤x≤70)天售价与销量的相关信息,得到如下统计表.
(1)求这种商品每天销售利润y(元)与时间x的函数解析式;时间x(天) 1≤x<40 40≤x≤70 售价(元/件) x+30 50 每天销量(件) 160-2x
(2)销售第几天,当天销售利润最大,并求出最大利润;
(3)在销售过程中,每天销售利润大于2250元共有多少天?发布:2025/5/24 20:0:2组卷:104引用:2难度:0.4 -
3.某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?发布:2025/5/24 20:0:2组卷:2657引用:119难度:0.1


