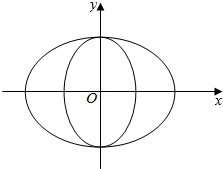
如图，曲线Γ由两个椭圆T1：x2a2+y2b2=1（a＞b＞0）和椭圆T2：y2b2+x2c2=1（b＞c＞0）组成，当a,b,c成等比数列时，称曲线Γ为“猫眼曲线”．
（1）若猫眼曲线Γ过点M（0，-2），且a,b,c的公比为22，求猫眼曲线Γ的方程；
（2）对于题（1）中的求猫眼曲线Γ，任作斜率为k（k≠0）且不过原点的直线与该曲线相交，交椭圆T1所得弦的中点为M，交椭圆T2所得弦的中点为N，求证：kOMkON为与k无关的定值；
（3）若斜率为2的直线l为椭圆T2的切线，且交椭圆T1于点A，B，N为椭圆T1上的任意一点（点N与点A，B不重合），求△ABN面积的最大值．
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
y
2
b
2
+
x
2
c
2
=
1
（
b
＞
c
＞
0
）
M
（
0
，-
2
）
2
2
k
OM
k
ON
2
【考点】椭圆的几何特征．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/12 16:0:8组卷：1008引用：9难度：0.5
相似题
-
1．阿基米德（公元前287年-公元前212年）不仅是著名的物理学家，也是著名的数学家，他利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积．若椭圆C的对称轴为坐标轴，焦点在x轴上，且椭圆C的离心率为
，面积为8π，则椭圆C的方程为（ ）32发布：2024/12/29 12:0:2组卷：229引用：7难度：0.5 -
2．已知椭圆C的两焦点分别为
、F1（-22，0），长轴长为6．F2（22，0）
（1）求椭圆C的标准方程；
（2）求以椭圆的焦点为顶点，以椭圆的顶点为焦点的双曲线的方程．发布：2024/12/29 11:30:2组卷：444引用：6难度：0.8 -
3．已知椭圆
=1（a＞b＞0）的一个焦点为F（2，0），椭圆上一点P到两个焦点的距离之和为6，则该椭圆的方程为（ ）x2a2+y2b2发布：2024/12/29 12:30:1组卷：12引用：2难度：0.7
