【问题】已知关于x的不等式ax2+bx+c＞0的解集是{x|1＜x＜2}，求关于x的不等式cx2+bx+a＞0的解集．
在研究上面的【问题】时，小明和小宁分别得到了下面的【解法一】和【解法二】：
【解法一】由已知得方程ax2+bx+c=0的两个根分别为1和2，且a＜0，
由韦达定理得1+2=-ba， 1×2=ca，
b=-3a, c=2a,
所以不等式cx2+bx+a＞0转化为2ax2-3ax+a＞0，整理得（x-1）（2x-1）＜0，解得12＜x＜1，所以不等式cx2+bx+a＞0的解集为{x|12＜x＜1}．
【解法二】由已知ax2+bx+c＞0得c（1x）2+b1x+a＞0，
令y=1x，则12＜y＜1，所以不等式cx2+bx+a＞0解集是{x|12＜x＜1}．
参考以上解法，解答下面的问题：
（1）若关于x的不等式kx+a+x+cx+b＜0的解集是{x|-2＜x＜-1或2＜x＜3}，请写出关于x的不等式kxax+1+cx+1bx+1＜0的解集；（直接写出答案即可）
（2）若实数m,n满足方程（m+1）2+（4m+1）2=1，（n+1）2+（n+4）2=n2，且mn≠1，求n3+m-3的值．
1 + 2 = - b a ， |
1 × 2 = c a ， |
b = - 3 a , |
c = 2 a , |
1
2
＜
x
＜
1
{
x
|
1
2
＜
x
＜
1
}
c
（
1
x
）
2
+
b
1
x
+
a
＞
0
y
=
1
x
1
2
＜
y
＜
1
{
x
|
1
2
＜
x
＜
1
}
k
x
+
a
+
x
+
c
x
+
b
＜
0
kx
ax
+
1
+
cx
+
1
bx
+
1
＜
0
【考点】类比推理；一元二次不等式及其应用．
【答案】（1）；
（2）-490．
（
-
1
，-
1
2
）
∪
（
1
3
，
1
2
）
（2）-490．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/12 7:0:8组卷：16引用：2难度：0.8
相似题
-
1．阅读下表后，请应用类比的思想，得出椭圆中的结论：
圆 椭圆 定
义平面上到动点P到定点O的距离等于定长的点的轨迹 平面上的动点P到两定点F1，F2的距离之和等于定值2a的点的轨迹（2a＞|F1F2|） 结
论如图，AB是圆O的直径，直线AC，BD是圆O过A，B的切线，P是圆O上任意一点，
CD是过P的切线，则有“PO2=PC•PD”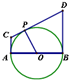
椭圆的长轴为AB，O是椭圆的中心，F1，F2是椭圆的焦点，直线AC，BD是椭圆过A，B的切线，P是椭圆上任意一点，CD是过P的切线，则有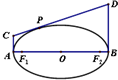 
发布：2025/1/28 8:0:2组卷：32引用：2难度：0.5 -
2．已知
tan（x+π4）=1+tanx1-tanx，那么函数y=tanx的周期为π．类比可推出：已知x∈R且（x≠kπ+π4），那么函数y=f（x）的周期是（ ）f（x+π）=1+f（x）1-f（x）发布：2025/1/6 8:0:1组卷：11引用：1难度：0.7 -
3．若
，x≠kπ+π4，则y=tanx的周期为π．类比可推出：设x∈R且tan（x+π4）=1+tanx1-tanx，则y=f（x）的周期是（ ）f（x+π）=1+f（x）1-f（x）发布：2025/1/6 8:0:1组卷：36引用：1难度：0.5
