苏科版教材八年级下册第94页第19题，小明在学过圆之后，对该题进行重新探究，请你和他一起完成问题探究．
【问题提出】如图1，点E，F分别在方形ABCD中的边AD、AB上，且BE=CF，连接BE、CF交于点M，求证：BE⊥CF．请你先帮小明加以证明．
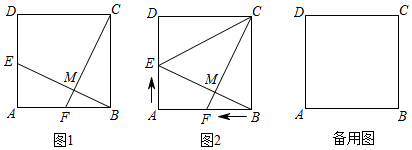
【问题探究】小明把原问题转化为动点问题，如图1，在边长为6cm的正方形ABCD中，点E从点A出发，沿边AD向点D运动，同时，点F从点B出发，沿边BA向点A运动，它们的运动速度都是2cm/s,当点E运动到点D时，两点同时停止运动，连接CF、BE交于点M，设点E，F运动时间为t秒．
（1）如图1，在点E、F的运动过程中，点M也随之运动，请直接写出点M的运动路径长 32π32πcm.
（2）如图2，连接CE，在点E、F的运动过程中．
①试说明点D在△CME的外接圆⊙O上；
②若①中的⊙O与正方形的各边共有6个交点，请直接写出t的取值范围．
3
2
π
3
2
π
【考点】圆的综合题．
【答案】
3
2
π
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/22 9:0:2组卷：356引用：3难度：0.2
相似题
-
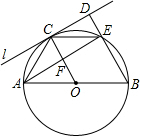1．如图，AB为⊙O的直径，C为半圆上一动点，过点C作⊙O的切线l,过点B作BD⊥l,垂足为D，BD与⊙O交于点E，连接OC，CE，AE，AE交OC于点F．
（1）求证：△CDE≌△EFC；
（2）若AB=4，连接AC．
①当AC=时，四边形OBEC为菱形；
②当AC=时，四边形EDCF为正方形．发布：2025/5/23 23:30:1组卷：963引用：8难度：0.5 -
2．如图①，已知⊙O是△ABC的外接圆，∠ABC=∠ACB=α（45°＜α＜90°，D为
上一点，连接CD交AB于点E．ˆAB
（1）连接BD，若∠CDB=40°，求α的大小；
（2）如图②，若点B恰好是中点，求证：CE2=BE•BA；ˆCD
（3）如图③，将CD分别沿BC、AC翻折得到CM、CN，连接MN，若CD为直径，请问是否为定值，如果是，请求出这个值，如果不是，请说明理由．ABMN
发布：2025/5/23 23:30:1组卷：1566引用：4难度：0.3 -
3．【问题提出】
（1）如图①，在Rt△ABC中，∠A=90°，AB=3，AC=4，点D是边BC上一动点，DE⊥AB于点E，DF⊥AC于点F，则EF的最小值为 ．
【问题探究】
（2）如图②，在△ABC中，∠A=45°，AB=4，AC=3，点D是BC边上一动点，DE⊥AB于点E，DF⊥AC于点F，⊙O是四边形AEDF的外接圆，求⊙O直径的最小值．2
【问题解决】
（3）某小区内有一块形状为四边形的空地，如图③所示，在四边形ABCD中，AD∥BC，∠C=90°，∠B=60°，AD=200米，AB=4003米，点E在CD上，且CE=2DE，F、G分别是边AB、BC上的两个动点，且∠FEG=60°．为了改善人居环境，小区物业准备在尽可能大的四边形BFEG区域内种植花卉，请问这个四边形BFEG区域的面积是否存在最大值？若存在，求出面积的最大值；若不存在，请说明理由．3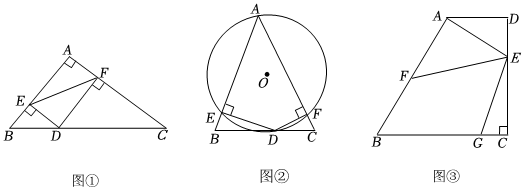
发布：2025/5/24 0:30:1组卷：570引用：3难度：0.1
