对于平面直角坐标系xOy中的任意一点P，给出如下定义：经过点P且平行于两坐标轴夹角平分线的直线，叫做点P的“特征线”．
例如：点M（1，3）的特征线是y=x+2和y=-x+4；
（1）若点D的其中一条特征线是y=x+1，则在D1（2，2）、D2（-1，0）、D3（-3，4）三个点中，可能是点D的点有D2D2；
（2）已知点P（-1，2）的平行于第二、四象限夹角平分线的特征线与x轴相交于点A，直线y=kx+b（k≠0）经过点P，且与x轴交于点B．若使△BPA的面积不小于6，求k的取值范围；
（3）已知点C（2，0），T（t,0），且⊙T的半径为1．当⊙T与点C的特征线存在交点时，直接写出t的取值范围．
【考点】圆的综合题．
【答案】D2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/12 12:0:9组卷：359引用：3难度：0.1
相似题
-
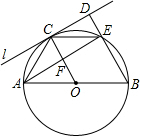1．如图，AB为⊙O的直径，C为半圆上一动点，过点C作⊙O的切线l,过点B作BD⊥l,垂足为D，BD与⊙O交于点E，连接OC，CE，AE，AE交OC于点F．
（1）求证：△CDE≌△EFC；
（2）若AB=4，连接AC．
①当AC=时，四边形OBEC为菱形；
②当AC=时，四边形EDCF为正方形．发布：2025/5/23 23:30:1组卷：963引用：8难度：0.5 -
2．如图①，已知⊙O是△ABC的外接圆，∠ABC=∠ACB=α（45°＜α＜90°，D为
上一点，连接CD交AB于点E．ˆAB
（1）连接BD，若∠CDB=40°，求α的大小；
（2）如图②，若点B恰好是中点，求证：CE2=BE•BA；ˆCD
（3）如图③，将CD分别沿BC、AC翻折得到CM、CN，连接MN，若CD为直径，请问是否为定值，如果是，请求出这个值，如果不是，请说明理由．ABMN
发布：2025/5/23 23:30:1组卷：1566引用：4难度：0.3 -
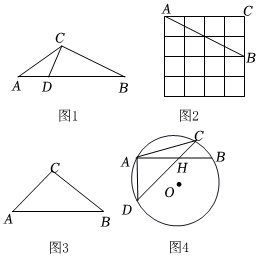3．【阅读理解】三角形一边上的点将该边分为两条线段，且这两条线段的积等于这个点到这边所对顶点连线的平方，则称这个点为三角形该边的“好点”．
如图1，△ABC中，点D是AB边上一点，连接CD，若CD2=AD•BD，则称点D是△ABC中AB边上的“好点”．
【探究应用】
（1）如图2，△ABC的顶点是4×4网格图的格点，请仅用直尺画出（或在图中直接描出）AB边上的“好点”；
（2）如图3，△ABC中，AB=14，cosA=，tanB=22，若点D是AB边上的“好点”，求线段AD的长；34
（3）如图4，△ABC是⊙O的内接三角形，点H在AB上，连接CH并延长交⊙O于点D，若点H是△ACD中CD边上的“好点”．
①求证：AH=BH；
②若BC⊥CH，⊙O的半径为r,且r=AD，求32的值．DHCH发布：2025/5/23 23:0:1组卷：1365引用：5难度：0.2
