某商品的进价为每件40元.当售价为每件60元时,每星期可卖出100件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出10件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
【考点】二次函数的应用.
【答案】(1)y=-10x2+100x+2000(0≤x<20);
(2)当降价5元时,每星期的利润最大,最大利润是2250元.
(2)当降价5元时,每星期的利润最大,最大利润是2250元.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/19 16:0:1组卷:245引用:3难度:0.6
相似题
-
1.奥运会主火炬手小王练习射箭点火,他需要用火种点燃箭头,然后准确地射向70米远、20米高的火炬塔,火炬塔上面是一个弓形的圣火台,该弓形的弦记为AB,且火炬塔EF垂直平分AB,这支箭飞行的运动轨迹可以看作是抛物线的一部分,记这支箭飞行的水平距离为d(单位:m),距地面的竖直高度为h(单位:m),获得数据如表:
小芳根据学习函数的经验,对函数h随自变量d的变化而变化的规律进行了研究,下面是小芳的探究过程,请补充完整:d(单位:m) 0 10 20 30 40 50 60 70 h(单位:m) 1.5 10.5 17.5 22.5 25.5 26.5 25.5 k
(1)k的值为 ;
(2)在平面直角坐标系中,描全以表中各对应值为坐标的点,并用平滑的曲线连接;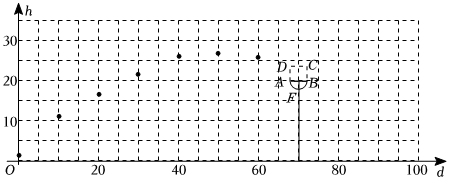
(3)只要小王射出箭的运动轨迹与线段AB有公共点(AB=4),那么这支箭就可以射入圣火台,请问小王是否可以将这支箭射入圣火台?答:(填“是”或者“否”)
(4)开幕式当晚,只要小王射出的箭能够进入圣火台上方边长为4米的正方形ABCD范围内(包含边界),都可以顺利点燃主火炬,小芳发现,在射箭的初始角度和力量不变的情况下,小王还可以通过调整与火炬塔的水平距离来改变这支箭的飞行轨迹(即向右平移原抛物线),若保证圣火被点燃,小王可以沿横轴正方向移动的最大距离是 米.(结果请保留根号)发布:2025/6/9 12:30:2组卷:168引用:2难度:0.5 -
2.某超市销售某种儿童玩具,每件进价为50元.根据市场调查发现:该玩具销售单价为100元时,每月的销售量为50件,而销售单价每降低1元,则每月可多售出5件.要求销售单价不得低于成本,且不高于110元.
(1)求该儿童玩具每月的销售量y(件)与销售单价x(元)之间的函数表达式;
(2)设超市每月销售这种玩具可获利W(元),当销售单价x为多少时W最大?W最大值是多少?发布:2025/6/9 14:30:1组卷:112引用:1难度:0.5 -
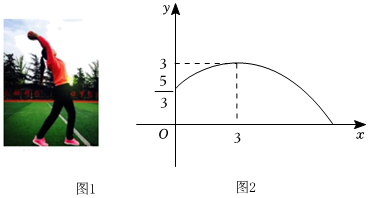 3.掷实心球是南宁市中考体育考试的项目.如图是一名女生掷实心球,实心球行进路线是一条抛物线,行进高度y m与水平距离x m之间的函数关系如图2所示,掷出时起点处高度为,当水平距离为3m时,实心球行进至最高点,此时距离地面3m.53m
3.掷实心球是南宁市中考体育考试的项目.如图是一名女生掷实心球,实心球行进路线是一条抛物线,行进高度y m与水平距离x m之间的函数关系如图2所示,掷出时起点处高度为,当水平距离为3m时,实心球行进至最高点,此时距离地面3m.53m
(1)求y关于x的函数表达式;
(2)南宁市体育中考评分标准(女生)如下表所示:
该女生在此项考试中获得多少分,请说明理由.成绩(分) 1 2 3 4 5 6 7 8 9 10 距离(米) 1.95 2.20 2.45 2.70 2.95 3.20 3.45 3.70 3.95 4.20 成绩(分) 11 12 13 14 15 16 17 18 19 20 距离(米) 4.70 5.10 5.50 5.90 6.30 6.70 7.10 7.50 7.90 8.30 发布:2025/6/9 12:0:2组卷:231引用:5难度:0.6


